نكته (قضيه‌ی سينوس‌ها): در هر مثلث، نسبت اندازه‌ی هر ضلع، به سينوس زاويه‌ی مقابل به آن، برابر است با قطر دايره‌ی محيطی مثلث. (R، شعاع دایره‌ی محیطی است.)

$\frac{a}{\operatorname{Sin}\hat{A}}=\frac{b}{\operatorname{Sin}\hat{B}}=\frac{c}{\operatorname{Sin}\hat{C}}=2R$

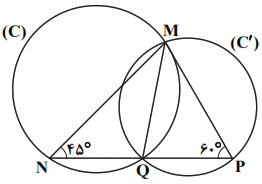
مطابق شکل، دایره‌ی $(C)$، دایره‌ی محیطی مثلث MNQ و دایره‌ی $({C}')$، دایره‌ی محیطی مثلث MPQ است. اگر شعاع دایره‌ی $(C)$ را R و شعاع دایره‌ی ${R}'$ در نظر بگیریم، با توجه به نکته، خواهیم داشت:

$\begin{align}
  & \left\{ \begin{matrix}
   \vartriangle MNQ:\frac{MQ}{\operatorname{Sin}\hat{N}}=2R\Rightarrow \frac{MQ}{\operatorname{Sin}{{45}^{{}^\circ }}}=2R\Rightarrow R=\frac{MQ}{2\times \frac{\sqrt{2}}{2}}=\frac{MQ}{\sqrt{2}}\,\,\,\,\,\,\,(1)  \\
   \vartriangle MPQ:\frac{MQ}{\operatorname{Sin}\hat{P}}=2{R}'\Rightarrow \frac{MQ}{\operatorname{Sin}{{60}^{{}^\circ }}}=2{R}'\Rightarrow {R}'=\frac{MQ}{2\times \frac{\sqrt{3}}{2}}=\frac{MQ}{\sqrt{3}}\,\,\,\,\,\,\,(2)  \\
\end{matrix} \right. \\ 
 & \xrightarrow{(1)\,\,,\,\,(2)}\,\frac{R}{{{R}'}}=\frac{\frac{MQ}{\sqrt{2}}}{\frac{MQ}{\sqrt{3}}}=\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{6}}{2}=\frac{1}{2}(\sqrt{6}) \\ 
\end{align}$

بنابراین گزینه‌ی 1 پاسخ است.