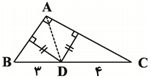
درس 3: قضیۀ نیمسازهای زوایای داخلی و محاسبۀ طول نیمسازها
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
نقطهای روی وتر مثلث قائم الزاويهای، از دو ضلع قائم آن به يک فاصله است. اگر اين نقطه، وتر را به دو پارهخط به طولهای 3 و 4 تقسيم كند، طول ضلع كوچک مثلث كدام است؟