درس 3: قضیۀ نیمسازهای زوایای داخلی و محاسبۀ طول نیمسازها
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
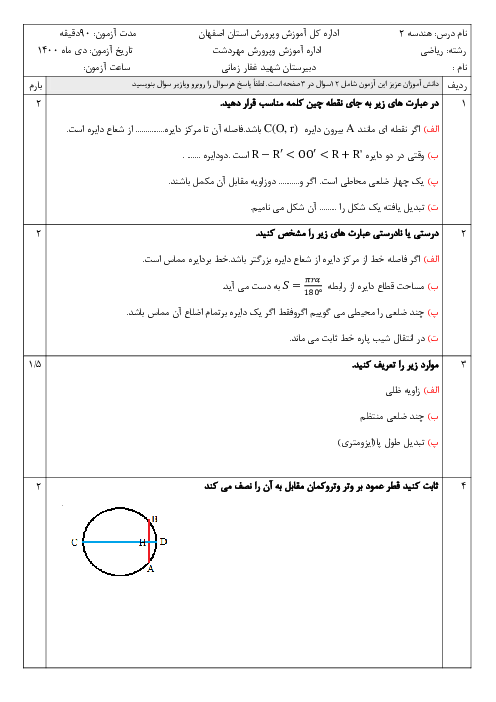
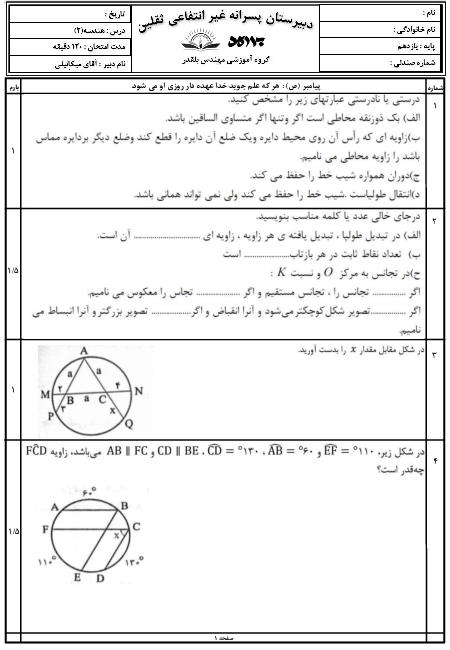
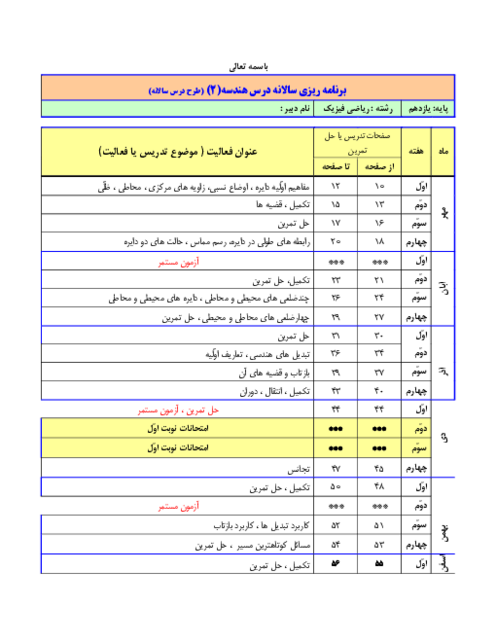
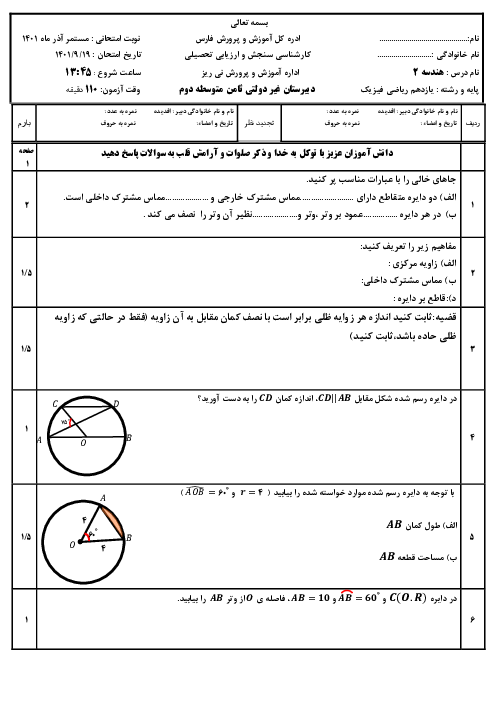
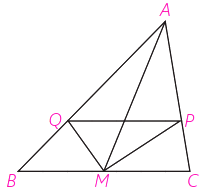
در مثلث ABC، نقطۀ M وسط BC است و MPو MQ نیمسازهای زوایای AMC و AMB هستند. کدام نتیجه‌گیری درست است؟
1 )
$\left. \begin{align}
& \frac{MA}{MC}=\frac{CP}{AP} \\
& \frac{MA}{MB}=\frac{QB}{AQ} \\
\end{align} \right\}\xrightarrow{MB=MC}\frac{AP}{PC}=\frac{AQ}{QB}\Rightarrow QP||BC$
2 )
$\left. \begin{align}
& \frac{MA}{MC}=\frac{AP}{PC} \\
& \frac{MA}{MB}=\frac{AQ}{QB} \\
\end{align} \right\}\xrightarrow{MB=MC}\frac{AP}{PC}=\frac{AQ}{QB}\Rightarrow MP||AB$
$\left. \begin{align}
& \frac{MA}{MC}=\frac{AP}{PC} \\
& \frac{MA}{MB}=\frac{AQ}{QB} \\
\end{align} \right\}\xrightarrow{MB=MC}\frac{AP}{PC}=\frac{AQ}{QB}\Rightarrow QP||BC$
4 )
$\left. \begin{align}
& \frac{MA}{MC}=\frac{CP}{AP} \\
& \frac{MA}{MB}=\frac{QB}{AQ} \\
\end{align} \right\}\xrightarrow{MB=MC}\frac{AP}{PC}=\frac{AQ}{QB}\Rightarrow QM||AC$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...