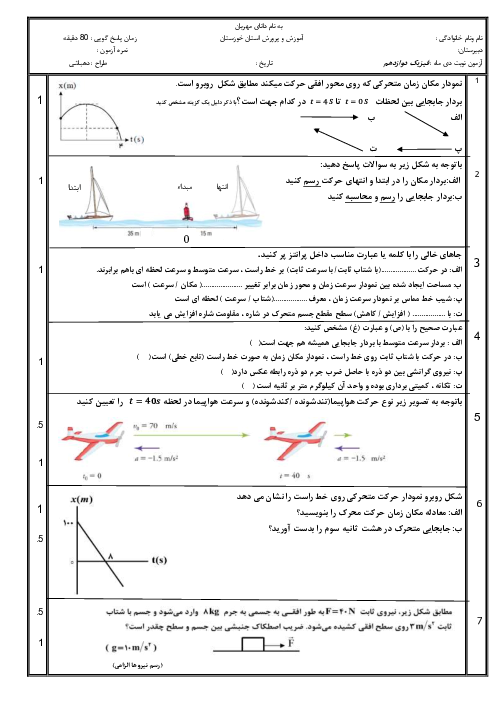
معادلات حركت هر دو متحرک را می‌نويسيم: 

متحرک $A$:

تا $t=1s$ ثانیهٔ دوم $t=2s$ 

 ${{({{v}_{av}})}_{A}}=\frac{\Delta x}{\Delta t}=\frac{0-(-20)}{2-1}=\frac{20}{1}=20\frac{m}{s},x={{({{v}_{av}})}_{A}}t+{{x}_{0}}$

با جای‌گذاری يكی از مكان‌ها و زمان‌های داده شده، مكان متحرک $A$ در لحظهٔ ${{t}_{0}}=0$ به‌دست می‌آید.

$\left. \begin{matrix} x=0  \\ t=2s  \\ \end{matrix} \right\}0=20\times 2+{{x}_{0}}\Rightarrow {{x}_{0}}=-40m$

بنابراين برای متحرک $A$ معادلهٔ حركت به‌صورت ${{x}_{A}}=20t-40$ خواهد بود.

متحرک $B$:

4 ثانیهٔ دوم: $t=4s$ تا $t=8s$ $\Rightarrow {{({{v}_{av}})}_{B}}=\frac{20-60}{8-4}=\frac{-40}{4}=-10\frac{m}{s}$

$\left. \begin{matrix} t=4s  \\ x=60m  \\ \end{matrix} \right\}\Rightarrow 60=-10\times 4+{{x}_{0}}\Rightarrow {{x}_{0}}=100m$

بنابراين معادلهٔ حركت متحرک $B$ به صورت ${{x}_{B}}=-10t+100$ خواهد بود. وقتی كه اين دو متحرک در يک مكان باشند بايد ${{x}_{A}}={{x}_{B}}$ شود، بنابراين داريم: 

${{x}_{A}}={{x}_{B}}\Rightarrow -10t+100=20t-40\Rightarrow 140=30t\Rightarrow t=\frac{14}{3}s$