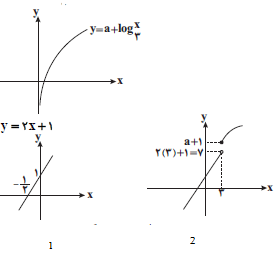
تابع $f(x)=\left\{ \begin{matrix}
   a-\log _{\frac{۱}{۳}}^{x}\,\,\,\,,\,\,\,x\ge ۳  \\
   ۲x+۱\,\,\,\,\,,\,\,\,\,x \lt ۳  \\
\end{matrix} \right.$ به ازای چه حدودی از $a$ همواره در شرط ${{x}_{۲}} \gt {{x}_{۱}}\Rightarrow f({{x}_{۲}})\ge f({{x}_{۱}})$ صدق می‌کند؟