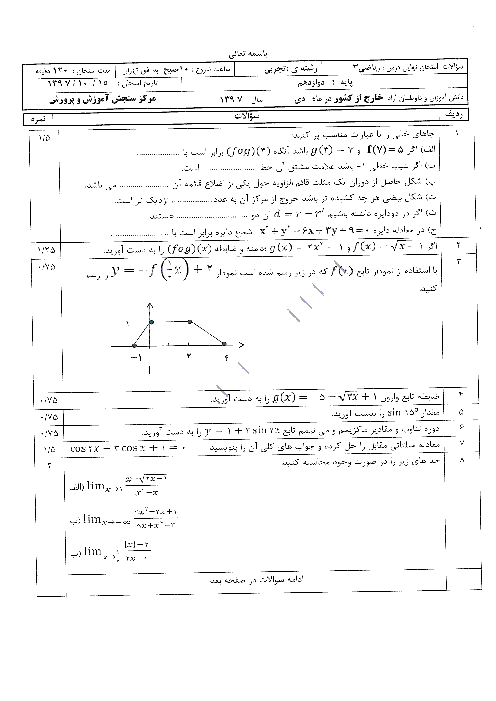
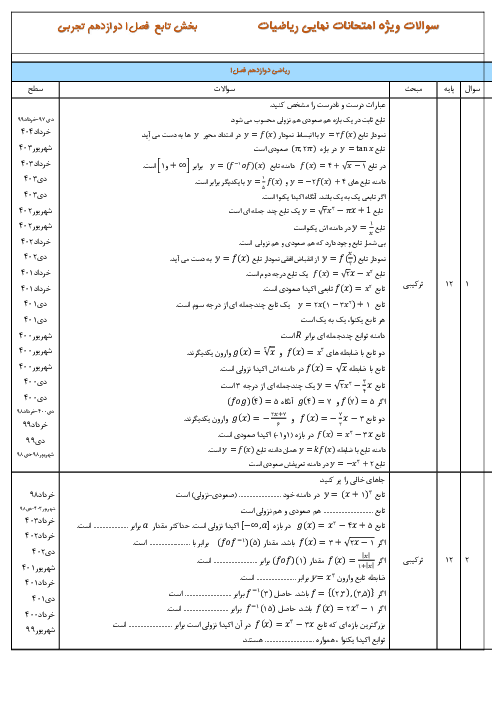
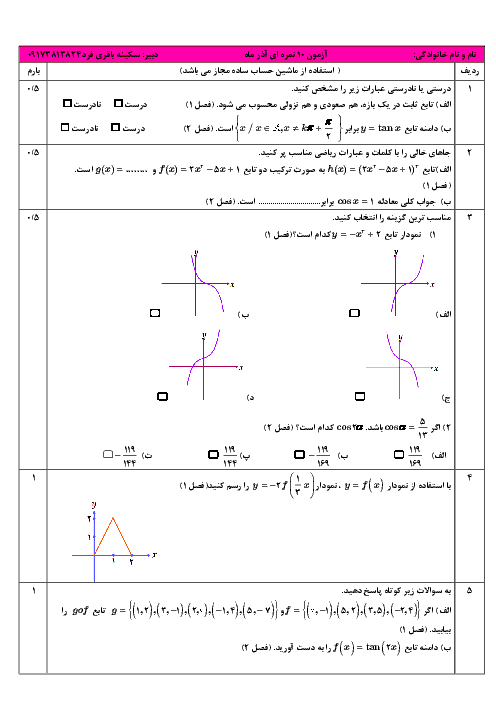
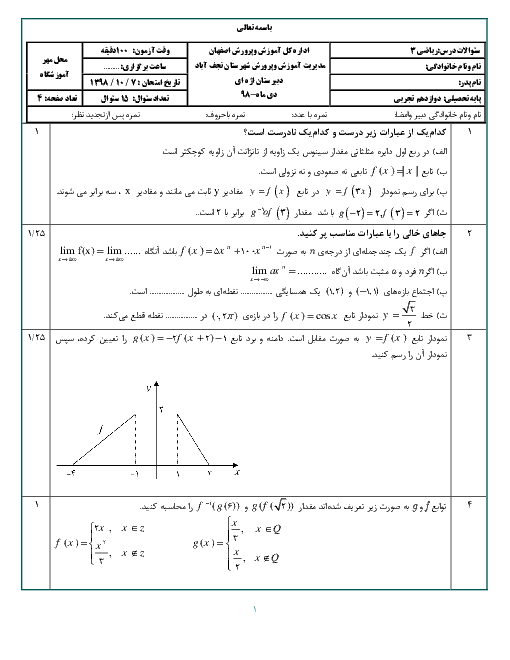
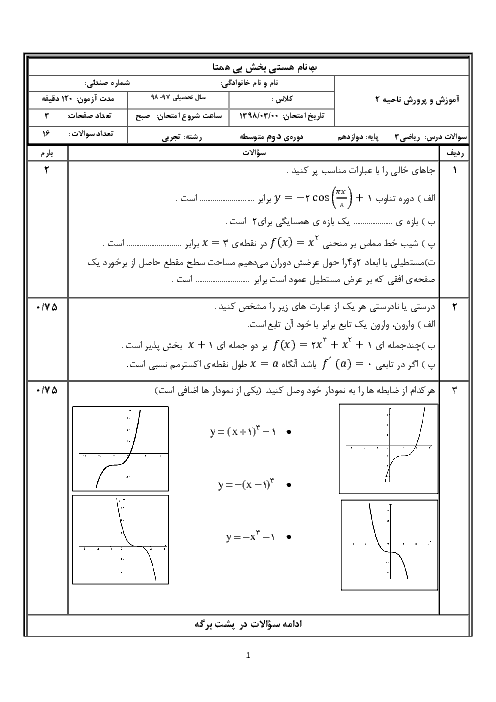
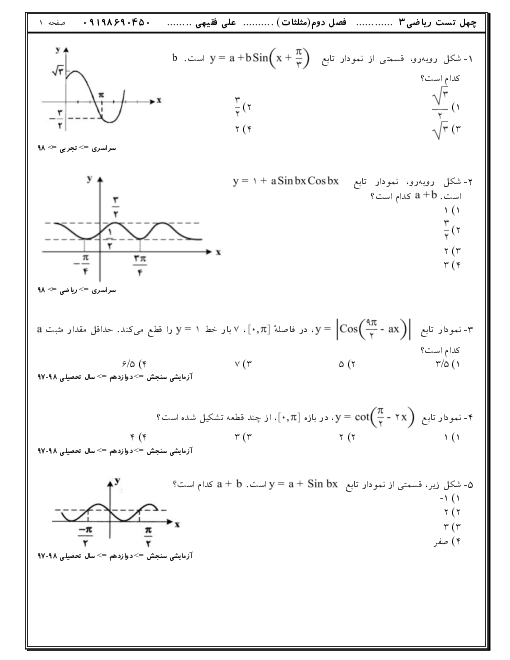
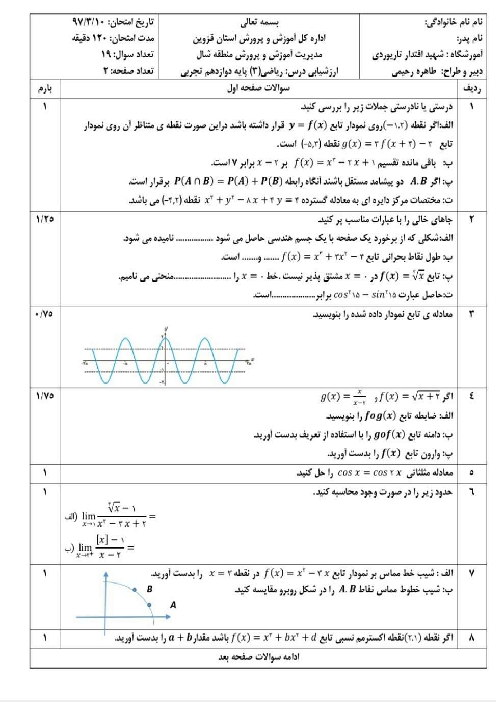
در یک کلاس $12$ نفره، $6$ نیمکت وجود دارد که روی هر نیمکت، دو دانش‌آموز نشسته است. اگر $3$ نفر به تصادف از دانش‌آموزان این کلاس انتخاب شود، احتمال آن‌که هیچ دو نفری از آن‌ها، از یک نیمکت نباشند کدام است؟
1 )
$\frac{2}{11}$
2 )
$\frac{4}{11}$
3 )
$\frac{6}{11}$
$\frac{8}{11}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...