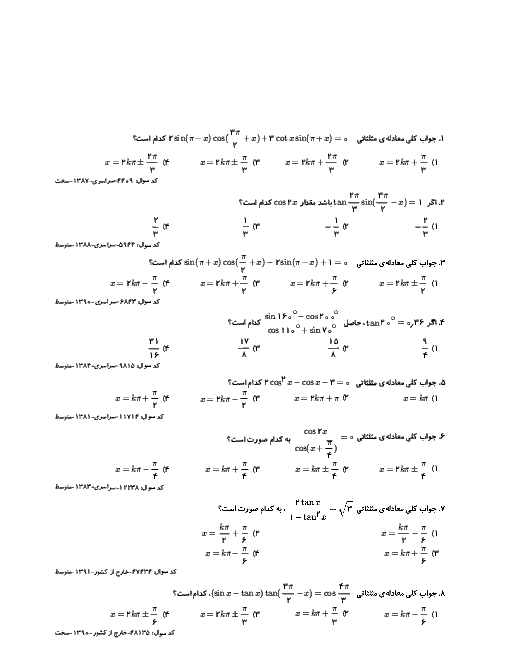نکته: توابع $y=a\operatorname{Sin}bx+c$ و $y=a\operatorname{Cos}bx+c$ دارای مقادیر ماکزیمم $\left| a \right|+c$ و مقدار مینیمم $-\left| a \right|+c$ و دورهٔ تناوب $\frac{2\pi }{\left| b \right|}$ است.
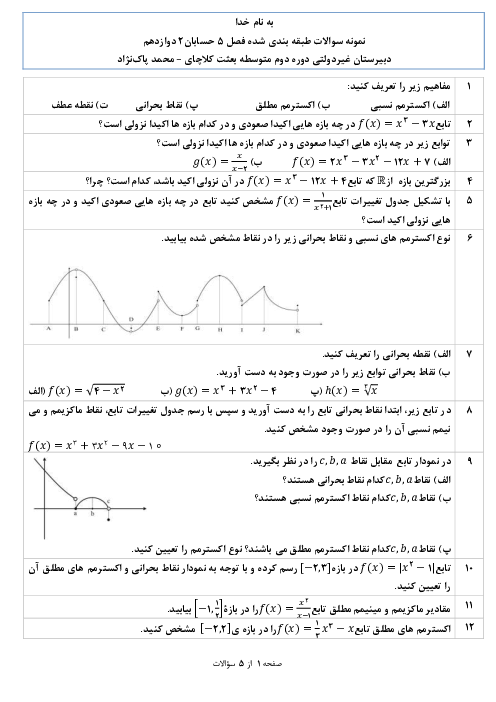
با توجه به صورت سؤال و نكته میتوان نوشت:
$\left\{ \begin{matrix} \left| a \right|+c=1 \\ -\left| a \right|+c=-7 \\ \frac{2\pi }{\left| b \right|}=4\pi \\ \end{matrix} \right.$
از جمع دو رابطۀ اول $c=-3$، از تفاضل آنها $\left| a \right|=4$ و از رابطۀ سوم، $\left| b \right|=\frac{1}{2}$ است.
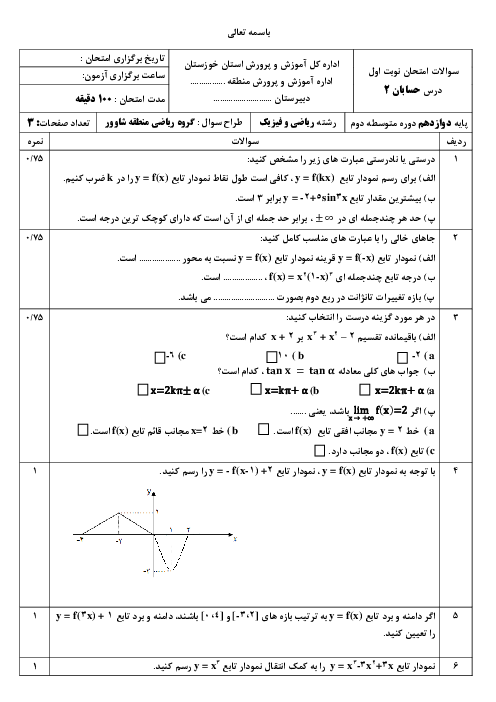
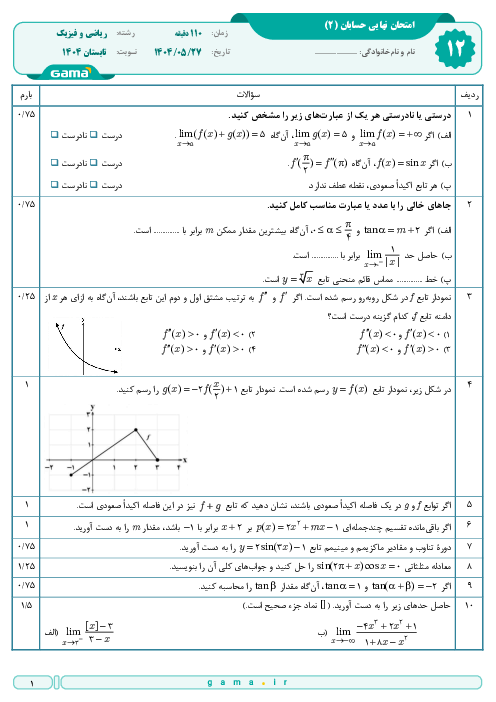
پس $y=4\operatorname{Cos}\frac{1}{2}x-3$ يكی از جوابهای مسئله است و گزينۀ ۲ پاسخ است.