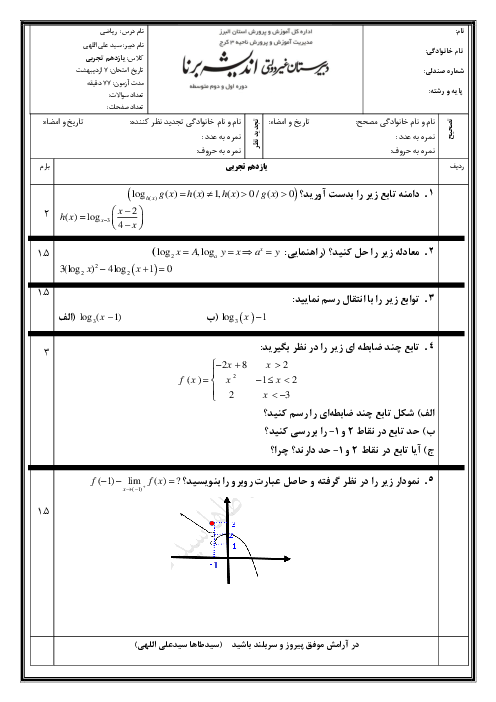
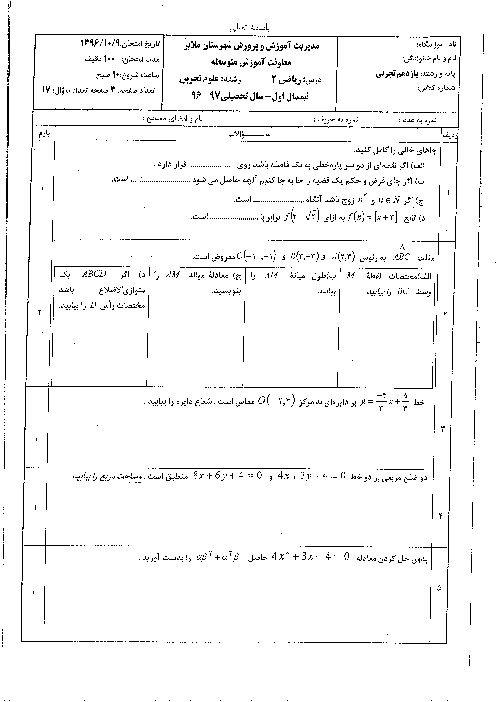
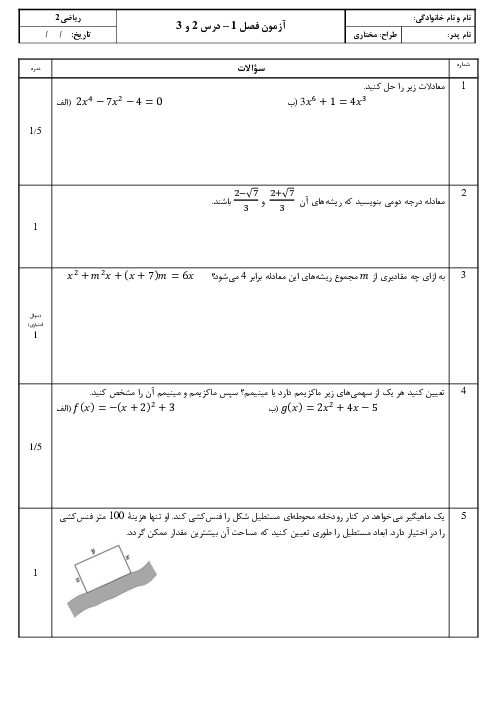
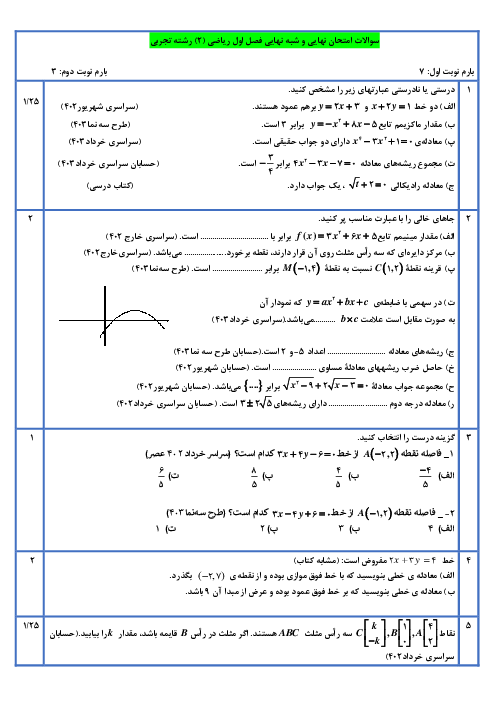
درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
معادلهٔ درجه دوم ${{x}^{2}}-({{m}^{2}}-3m+3)x+{{m}^{3}}-3=0$ دارای دو ریشهٔ حقیقی متمایز است. اگر مجموع ریشههای این معادله برابر 1 باشد، حاصل ضرب ریشههای این معادله کدام است؟