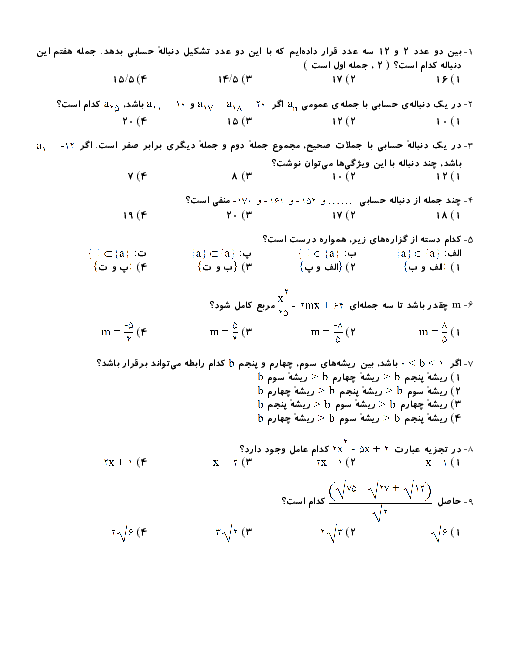فرض کنید $A = \left[ {\begin{array}{*{20}{c}}\begin{array}{l}\frac{3}{4}\\2\end{array}&\begin{array}{l}\frac{1}{2}\\1\end{array}\end{array}} \right]$ و ماتریس $X$، جواب معادلهٔ $AX = {A^{ - 1}}$، باشد. ماتریس $X$، کدام است؟
1 )
$\left[ {\begin{array}{*{20}{c}}{ - 32}\\{48}\end{array}\,\,\,\,\,\,\begin{array}{*{20}{c}}{14}\\{ - 25}\end{array}} \right]$
$\left[ {\begin{array}{*{20}{c}}{32}\\{ - 56}\end{array}\,\,\,\,\,\,\begin{array}{*{20}{c}}{ - 14}\\{25}\end{array}} \right]$
3 )
$\left[ {\begin{array}{*{20}{c}}{16}\\{ - 28}\end{array}\,\,\,\,\,\,\begin{array}{*{20}{c}}{ - 7}\\{21}\end{array}} \right]$
4 )
$\left[ {\begin{array}{*{20}{c}}{16}\\{ - 25}\end{array}\,\,\,\,\,\,\begin{array}{*{20}{c}}{ - 7}\\{14}\end{array}} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!