در شکل زیر و می‌باشد. اگر و مساحت مثلث برابر باشد، مساحت چهارضلعی کدام است؟

موبایل / ایمیل

قوانین و مقررات را خواندم و می پذیرم.

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

موبایل / ایمیل

ورود | ثبت نام

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

انصراف

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

درس 4: کاربردهایی از قضیۀ تالس و تشابه مثلث‌ها هندسه (1) دهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

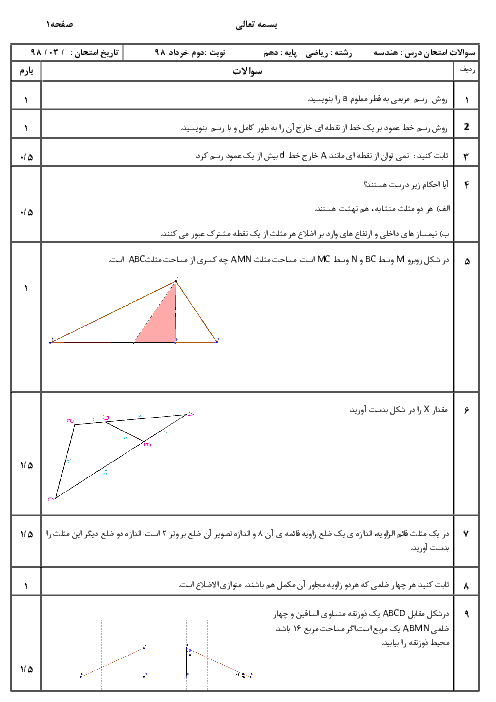
در شکل زیر $A\hat{F}E=A\hat{C}B$ و $C\hat{A}D=D\hat{A}B$ می‌باشد. اگر $AL=LD$ و مساحت مثلث $AFE$ برابر $2$ باشد، مساحت چهارضلعی $BCEF$ کدام است؟

1 )

$4$

2 )

$6$

3 )

$8$

4 )

$9$

نمایش پاسخ

در مثلث $AFE$ و $ABC$ با دو زاویهٔ برابر متشابه‌اند. بنابراین نسبت تشابه آن‌ها برابر نسبت تشابه نیمسازهای متناظر آن‌هاست. چون $AD$ (نیمساز مثلث $ABC$) دو برابر $AL$ (نیمساز مثلث $AFE$) می‌باشد، پس نسبت تشابه دو مثلث $2$ می‌باشد و در نتیجه نسبت مساحت‌های آن‌ها برابر ${{2}^{2}}=4$ است و داریم:

$\frac{{{S}_{ABC}}}{{{S}_{AFE}}}=4\Rightarrow \frac{{{S}_{ABC}}}{2}=4\Rightarrow {{S}_{ABC}}=8\Rightarrow {{S}_{BCEF}}={{S}_{ABC}}-{{S}_{AFE}}=8-2=6$

گزارش خطا

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مرتبط