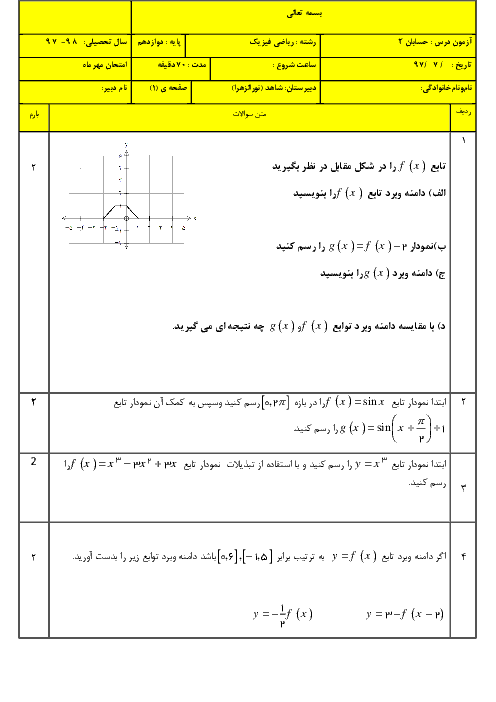
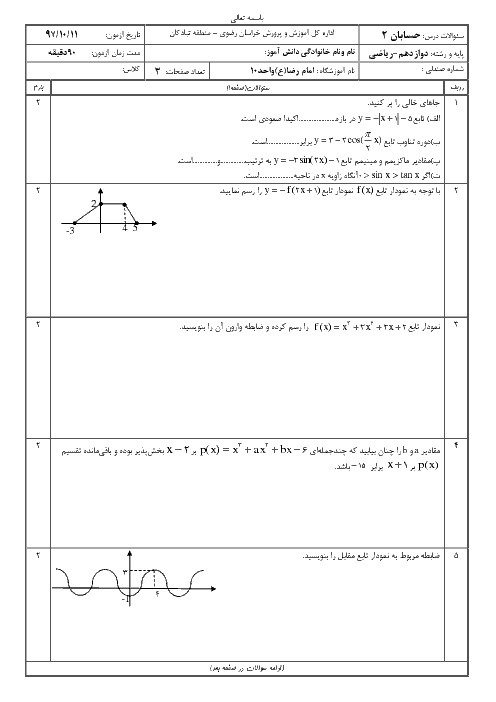
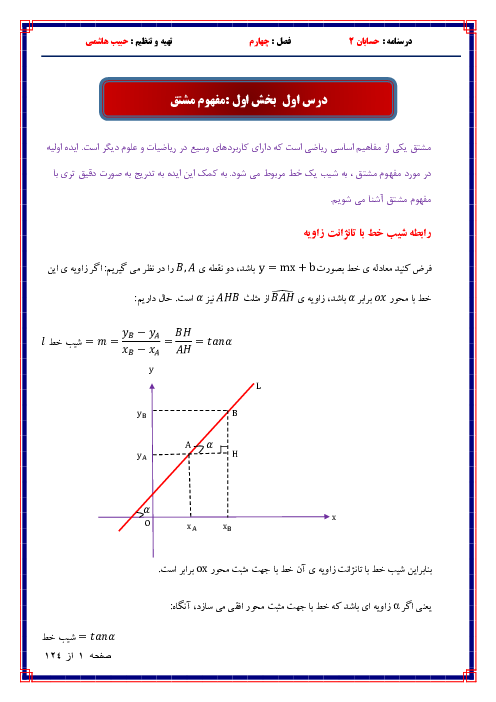
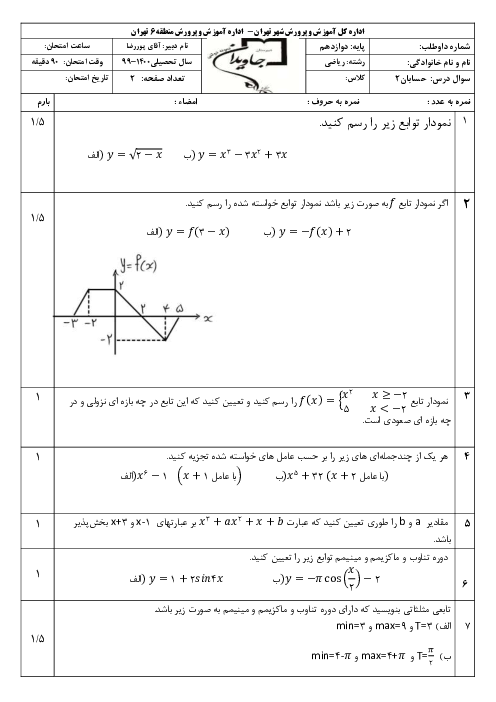
ابتدا طرفین وسطین میکنیم، داریم:
$(1+\cos x)(1-\cos x)=\sin x.\cos \frac{x}{2}\Rightarrow 1-{{\cos }^{2}}x=\sin x.\cos \frac{x}{2}$
$\begin{align} & \Rightarrow {{\sin }^{2}}x-\sin x.\cos \frac{x}{2}\Rightarrow \sin x(\sin x-\cos \frac{x}{2})=0 \\ & \sin x=0\Rightarrow x=k\pi ,\sin x-\cos \frac{x}{2}=0 \\ & \Rightarrow \sin x=\cos \frac{x}{2} \\ & \Rightarrow \sin x=\sin (\frac{\pi }{2}-\frac{x}{2}) \\ \end{align}$
$\Rightarrow \left\{ \begin{align} & x=2k\pi +(\frac{\pi }{2}-\frac{x}{2})\Rightarrow x=\frac{4k\pi }{3}+\frac{\pi }{3} \\ & x=2k\pi +\pi -(\frac{\pi }{2}-\frac{x}{2})\Rightarrow x=4k\pi +\pi \\ \end{align} \right.$