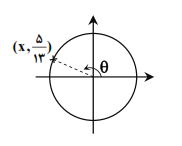
نکته: مختصات نقطه‌ی $P(x,y)$ متناظر با زاویه‌ی $\theta$ روی دایره‌ی مثلثاتی به صورت $x=\cos \theta$ و $y=\sin \theta$ است.

مطابق نکته، $P(x, \frac{5}{13})$ روی دایره‌ی مثلثاتی و متناظر با زاویه‌ی $\theta$ است، پس $\sin \theta= \frac {5}{13}$

برای بدست آوردن مقدار $\cot \theta$ دو راه حل ارائه می‌کنیم:

راه حل اول:

نکته: $1+{{\cot }^{2}}\theta =\frac{1}{{{\sin }^{2}}\theta }$

$1+{{\cot }^{2}}\theta =\frac{1}{{{\sin }^{2}}\theta }\,\Rightarrow \,1+{{\cot }^{2}}\theta =\frac{1}{\frac{25}{169}}\Rightarrow {{\cot }^{2}}\theta =\frac{169}{25}-1\,\Rightarrow {{\cot }^{2}}\theta =\frac{144}{25}\Rightarrow \cot \,\theta =\pm \frac{12}{5}$

با توجه به اینکه $\theta$ در ربع دوم است، $\cot \theta$ مقداری منفی است، پس:

$\cot \theta =- \frac {12}{5}=-2/4$

راه ‌حل دوم:

نکته:‌ $\cot \,\theta =\frac{\cos \theta }{\sin \theta }\,\,\,,\,\,\,{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$

ابتدا به کمک نکته مقدار $\cos \theta$ را به دست می‌آوریم:

$\sin \,\theta =\frac{5}{13}\,\Rightarrow {{(\frac{5}{13})}^{2}}+{{\cos }^{2}}\theta =1\,\Rightarrow \,{{\cos }^{2}}\theta =1-\frac{25}{169}\Rightarrow {{\cos }^{2}}\theta =\frac{144}{169}\Rightarrow \cos \,\theta =\pm \frac{12}{13}$

چون $\theta$ در ربع دوم قرار دارد و مقدار $\cos \theta$ در ربع دوم منفی است، پس $\cos \theta =-\frac {12}{13}$

بنابراین: $\cos \,\theta =\frac{-\frac{12}{13}}{\frac{5}{13}}=-\frac{12}{5}=-2/4$