قايقی برای بررسی لايه‌های كف اقيانوسی از ارسال موج‌های صوتی استفاده می‌كند. موجی كه از روی سطح گِلی باز می‌تابد در مدت پس از ارسال دريافت می‌شود. موجی كه از روی… | فیزیک (3) تجربی دوازدهم شماره 84675

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 6: مشخصه‌های موج فیزیک (3) تجربی دوازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

قايقی برای بررسی لايه‌های كف اقيانوسی از ارسال موج‌های صوتی استفاده می‌كند. موجی كه از روی سطح گِلی باز می‌تابد در مدت ${{t}_{1}}=0/1s$ پس از ارسال دريافت می‌شود. موجی كه از روی سطح سنگی باز می‌تابد در مدت ${{t}_{2}}=0/12s$ پس از ارسال، دريافت می‌شود. اگر تندی صوت در گِل $1875\frac{m}{s}$ باشد، ضخامت لايهٔ گِلی چند متر است؟

1 )

7/5

2 )

9/38

3 )

18/75

4 )

37/5

نمایش پاسخ

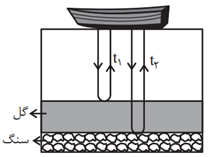
زمان رفت موج از سطح آب تا سطح گِل و برگشت آن به نقطهٔ اوليه ${{t}_{1}}$ است که مسافت $2{{h}_{1}}$ را طی می‌کند و چون با تندی ثابت صورت می‌گيرد، داريم:

$\Delta x=v\Delta t\Rightarrow 2{{h}_{1}}={{v}_{1}}\Delta {{t}_{1}}\Rightarrow 2{{h}_{1}}={{v}_{1}}\times \frac{1}{10}\Rightarrow {{v}_{1}}=20{{h}_{1}}$

برای حالت دوم داريم:

$\Rightarrow \Delta x=v\Delta t\Rightarrow \Delta t=\frac{\Delta x}{v}$

$\Delta {{t}_{2}}=\frac{\Delta {{x}_{1}}}{{{v}_{1}}}+\frac{\Delta {{x}_{2}}}{{{v}_{2}}}\Rightarrow 0/12=\frac{2{{h}_{1}}}{{{v}_{1}}}+\frac{2{{h}_{2}}}{v}$

$0/12=\frac{2{{h}_{1}}}{20{{h}_{1}}}+\frac{2{{h}_{2}}}{1875}\Rightarrow \frac{2{{h}_{2}}}{1875}=0/12-0/1$

$\frac{2{{h}_{2}}}{1875}=0/02\Rightarrow {{h}_{2}}=18/75m$

گزارش اشکال