درس 2: جهت تقعر نمودار یک تابع و نقطۀ عطف آن
حسابان (2)
دوازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
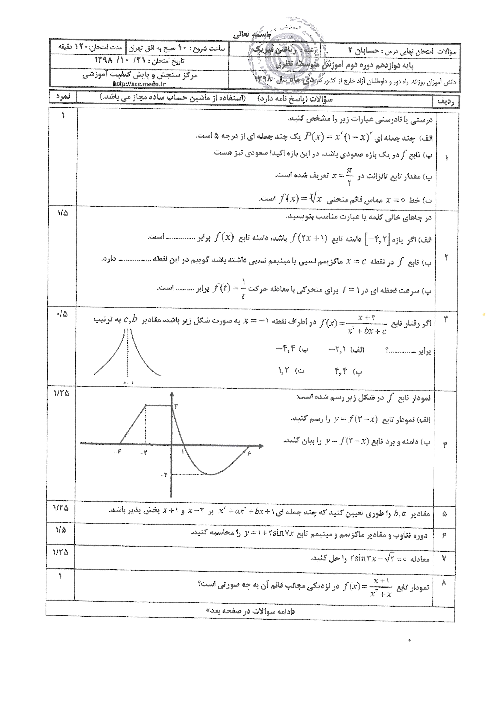
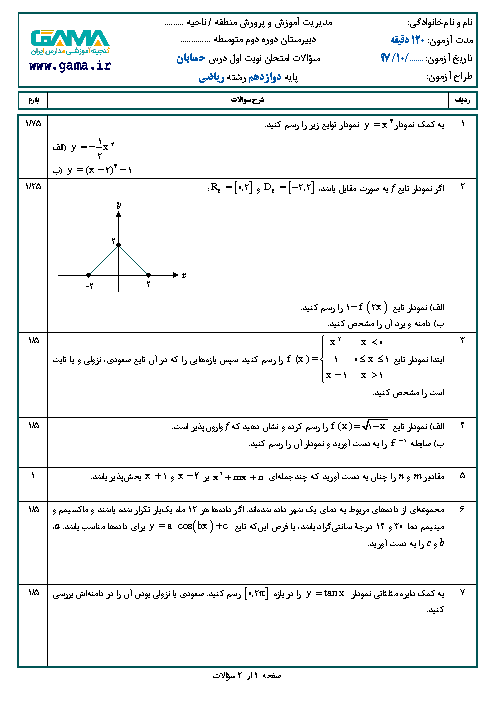
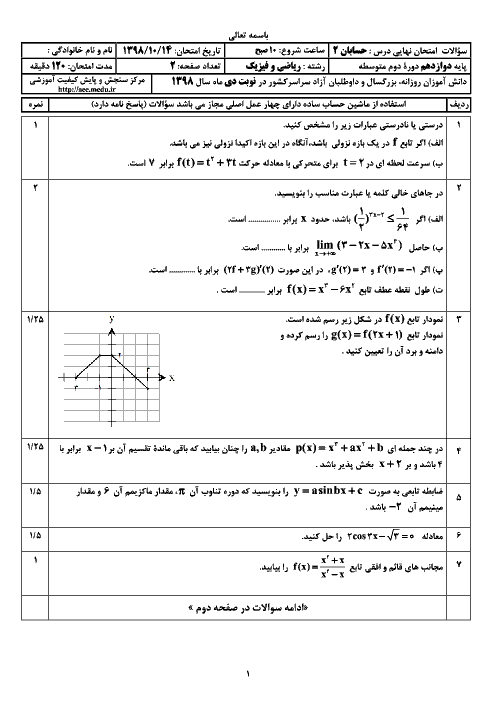
خطوط مماس در نقاط عطف تابع $y=\operatorname{Sin}2x$ در بازهٔ $(0,\frac{3\pi }{2})$ يكديگر را روی خط $y=k$ قطع میكنند. $k$ كدام است؟