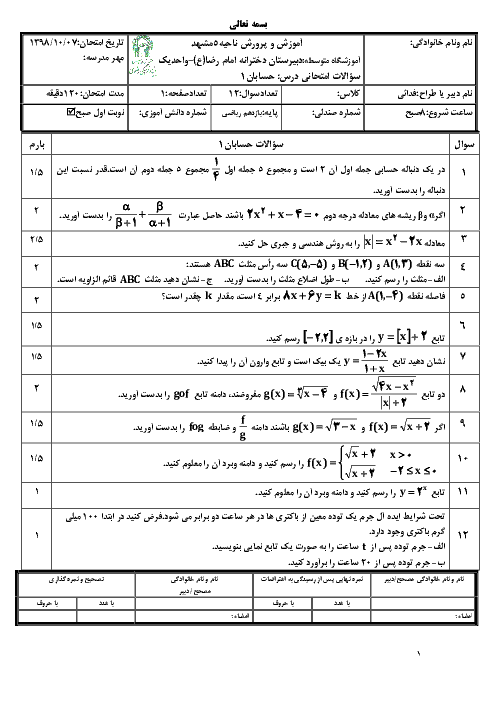
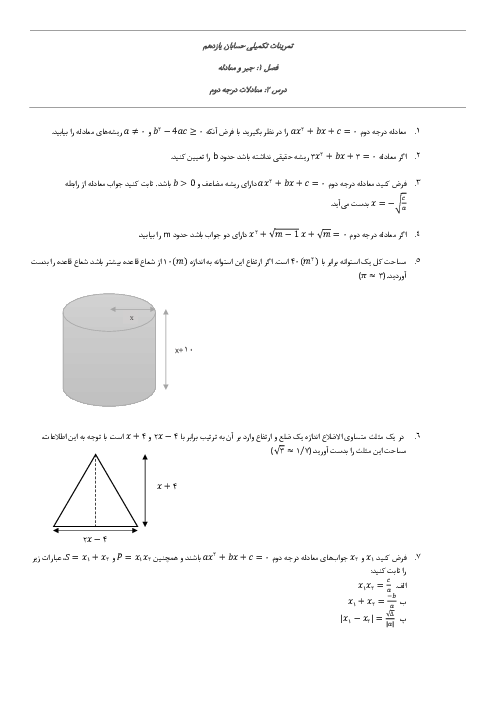
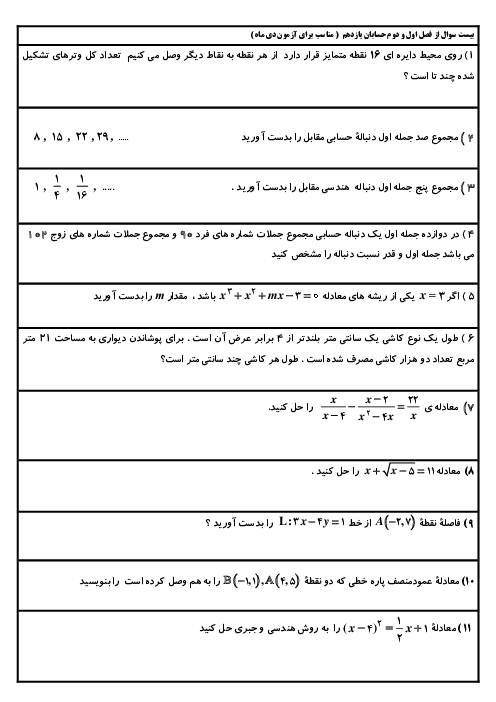
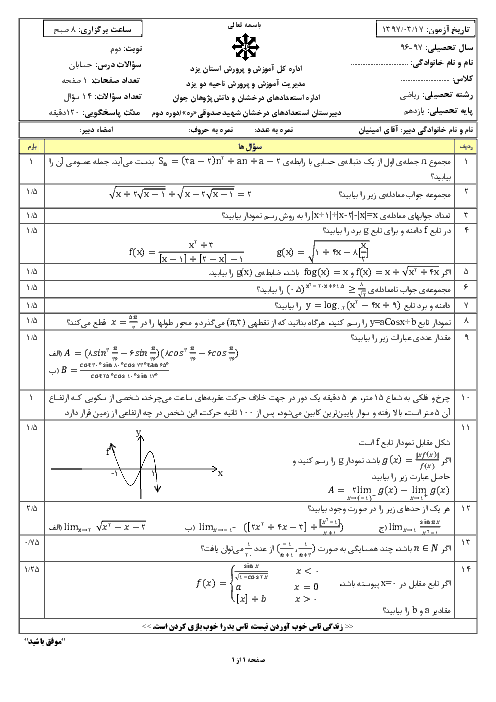
خطی که از نقطه‌ای به طول $-\frac{3}{2}$ واقع بر تابع $f(x)=[3x]$ می‌گذرد و محور طول‌ها را در نقطه‌ای به طول 2/5- قطع می‌کند، از کدام نقطهٔ زیر می‌گذرد؟ ($\left[ {} \right]$، نماد جزء صحیح است.)
1 )
$(\frac{3}{2},10)$
$(\frac{1}{2},15)$
3 )
$(\frac{5}{2},-10)$
4 )
$(\frac{1}{2},15)$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...