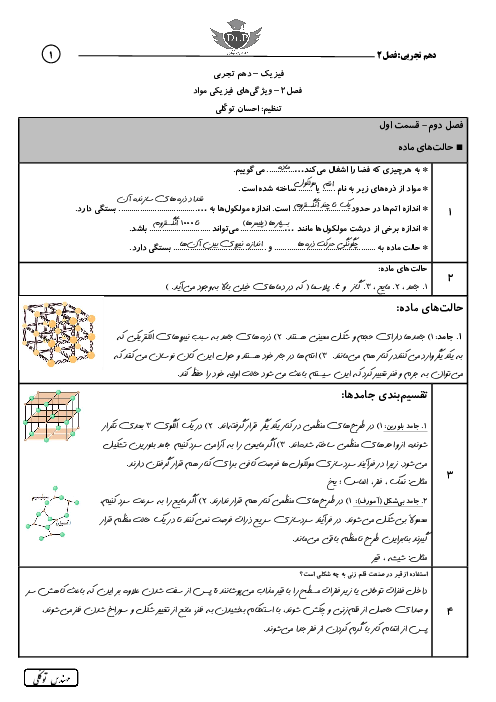
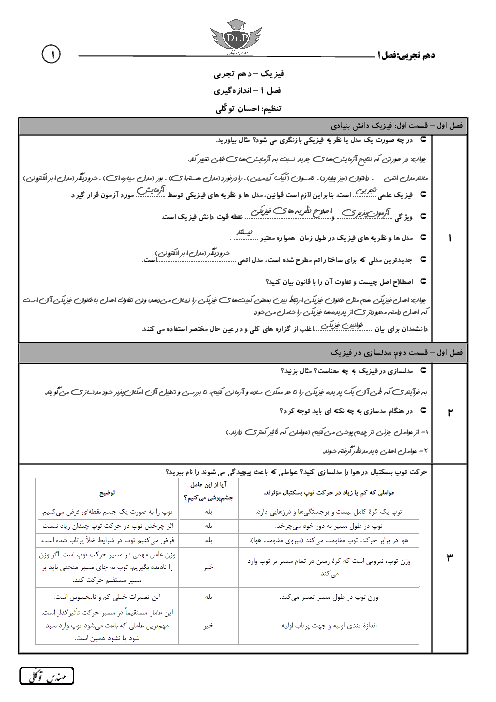
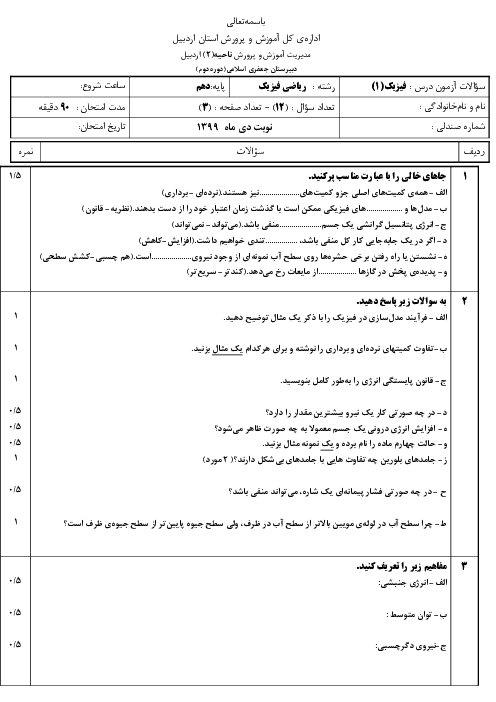
ظرف پر از مایعی به چگالی $1/2\frac{g}{c{{m}^{3}}}$ در اختیار داریم. جسمی به جرم ۲۰۰ گرم را به طور کامل درون ظرف قرار می‌دهیم. اگر ۶۰ گرم از مایع درون ظرف سرریز شود، آنگاه: $({{\rho }_{jesm}}=5\frac{g}{c{{m}^{3}}})$
1 )
جسم توپر بوده است.
2 )
درون جسم حفره‌ای به حجم 50 سانتی‌متر مکعب وجود داشته است.
درون جسم حفره‌ای به حجم 10 سانتی‌متر مکعب وجود داشته است.
4 )
درون جسم حفره‌ای به حجم 240 سانتی‌متر مکعب وجود داشته است.
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...