** فصل 1: ماتریس و کاربردها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
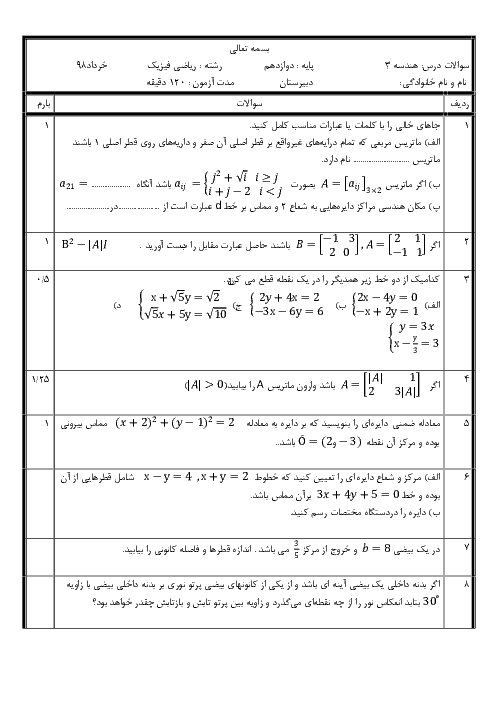
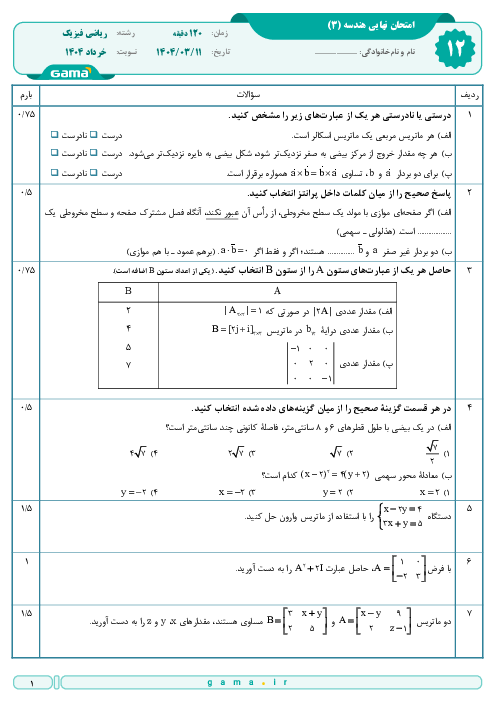
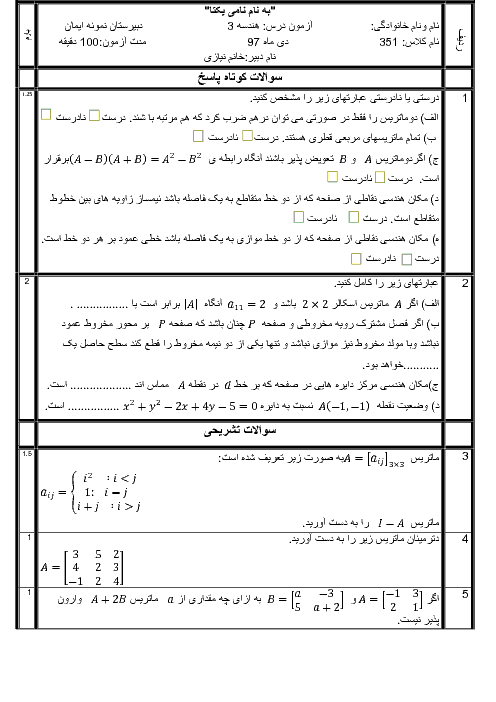
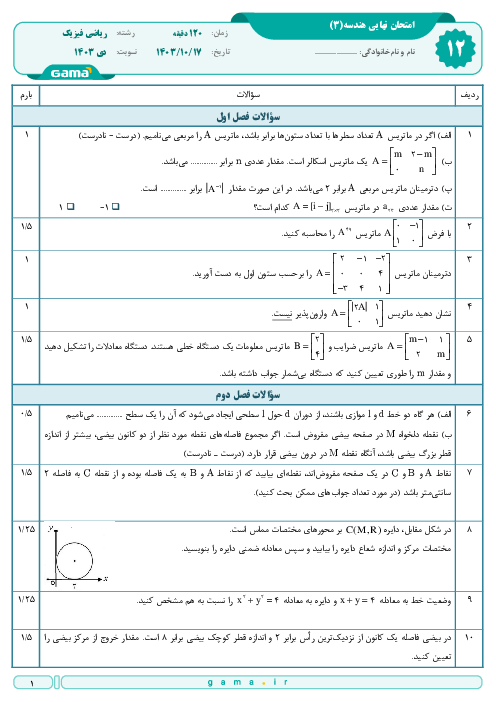
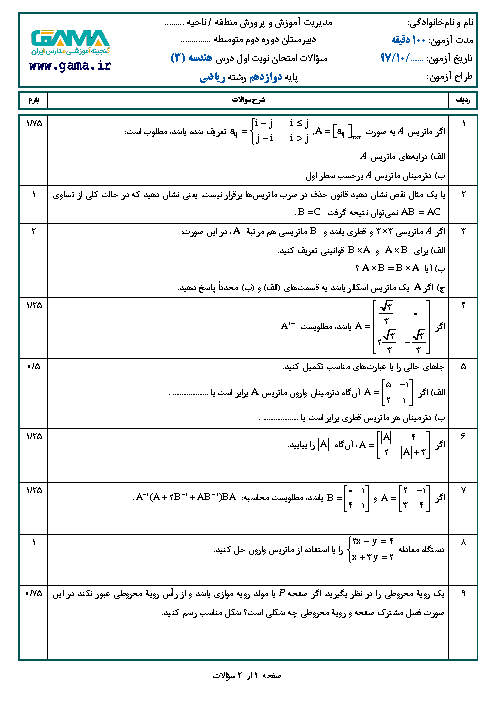
دترمینال کدام‌یک از ماتریس‌های زیر برابر با صفر نیست؟ $(a,b,x,y,z\in R)$
1 )
$\left[ \begin{matrix} 3 & 2 & -1 \\ -6 & 1 & 2 \\ 1 & 5 & -\frac{1}{3} \\ \end{matrix} \right]$
2 )
$\left[ \begin{matrix} a & a & a \\ x & y & z \\ b & b & b \\ \end{matrix} \right]$
$\left[ \begin{matrix} 2 & 1 & -1 \\ -1 & 1 & 2 \\ 3 & 4 & 9 \\ \end{matrix} \right]$
4 )
$\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
محمدجواد باغبان باشی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...