وارون پذیری تابع $f(x) = - \left| {x - 1} \right| + 1$ را با شرط $x \geqslant 1$ بررسی کنید و در صورت وارون پذیر بودن، دامنه و ضابطهٔ وارون آن را به دست آورید.
پاسخ تشریحی :
نمایش پاسخ
چون $x \geqslant 1$ است، پس حاصل $(x - 1)$ نامنفی بوده و خودش از قدرمطلق خارج میشود:
$f(x) = - (x - 1) + 1 = - x + 1 + 1 = - x + 2$
با رسم نمودار، معلوم میشود که تابع f یک به یک و در نتیجه وارون پذیر است. (شکل)
$y = - x + 2 \to x = 2 - y \to {f^{ - 1}}(x) = 2 - x$
ضمناً از روی نمودار متوجه میشوید که برد آن $\left( { - \infty ,1} \right]$ است، پس دامنهٔ ${f^{ - 1}}$ هم برابر همین بازه است.
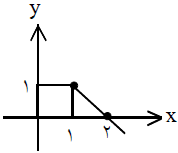
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...