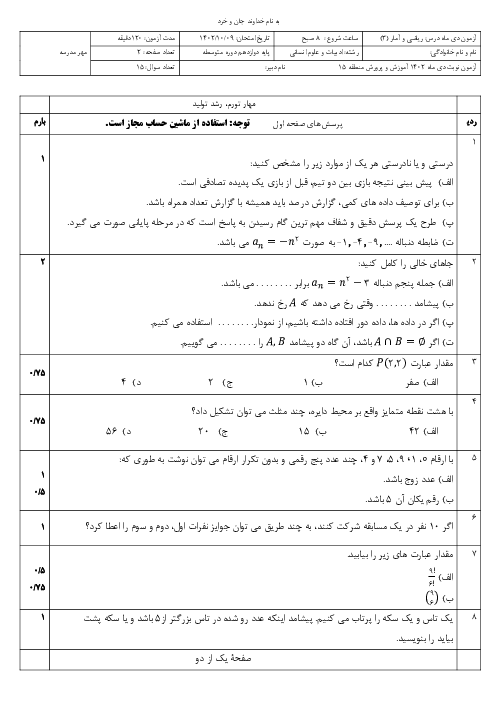
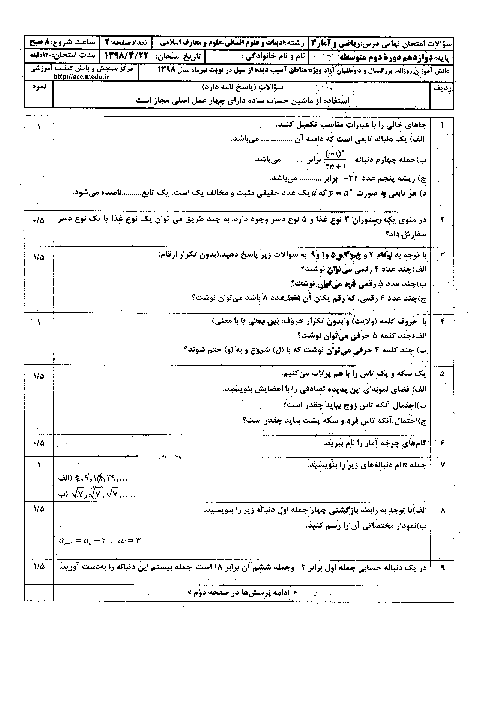
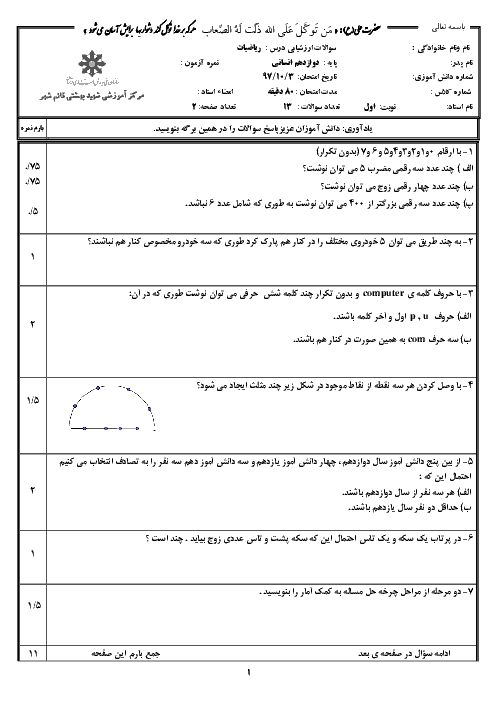
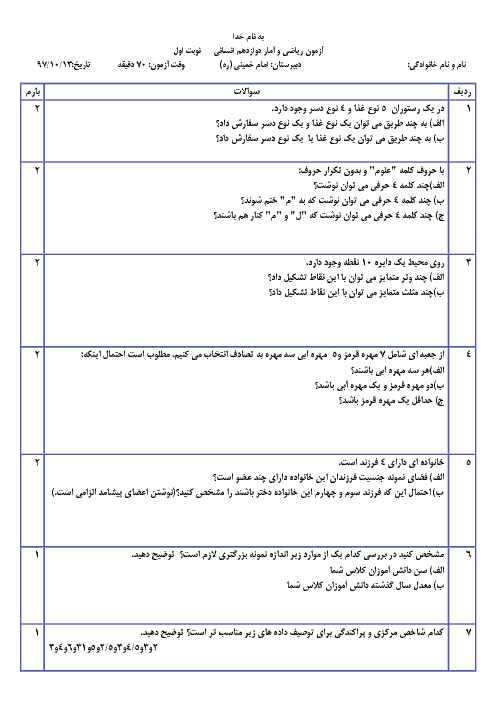
مجموع جملات ششم و هفتم برابر $31$ است، پس:

${{a}_{6}}+{{a}_{7}}=31\Rightarrow {{a}_{1}}+5d+{{a}_{1}}+6d=31\Rightarrow 2{{a}_{1}}+11d=31$

مجموع جملات دوم تا چهارم $15$ است، پس: ${{a}_{2}}+{{a}_{3}}+{{a}_{4}}=15$

$\Rightarrow {{a}_{1}}+d+{{a}_{1}}+2d+{{a}_{1}}+3d=15\Rightarrow 3{{a}_{1}}+6d=15$

در معادلهٔ دوم، دو طرف را بر $3$ تقسیم می‌کنیم:

$3{{a}_{1}}+6d=15\xrightarrow{\div 3}{{a}_{1}}+2d=5$

حالا دو معادلهٔ $2{{a}_{1}}+11d=31$ و ${{a}_{1}}+2d=5$ را در یک دستگاه حل می‌کنیم:

$\begin{align}
& \left\{ \begin{matrix}
2{{a}_{1}}+11d=31  \\
{{a}_{1}}+2d=5\,\,\,\,\,\,\,  \\
\end{matrix} \right.\,\,\,\,\begin{matrix}
\xrightarrow{{}}  \\
\xrightarrow{\times (-2)}  \\
\end{matrix}\,\,\underline{\left\{ \begin{matrix}
2{{a}_{1}}+11d=31  \\
-2{{a}_{1}}-4d=-10  \\
\end{matrix} \right.\,}\,\,\oplus  \\
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7d=21\Rightarrow d=\frac{21}{7}=3 \\
\end{align}$

حالا $d=3$ را در معادلهٔ ${{a}_{1}}+2d=5$ قرار می دهیم تا ${{a}_{1}}$ به دست ‌آید:

${{a}_{1}}+2d=5\xrightarrow{d=3}{{a}_{1}}+\underbrace{2(3)}_{6}=5\Rightarrow {{a}_{1}}=-1$

با داشتن ${{a}_{1}}=-1$ و $d=3$، جملهٔ پنجم را به دست می‌آوریم:

${{a}_{5}}={{a}_{1}}+4d=-1+4(3)=-1+12=11$