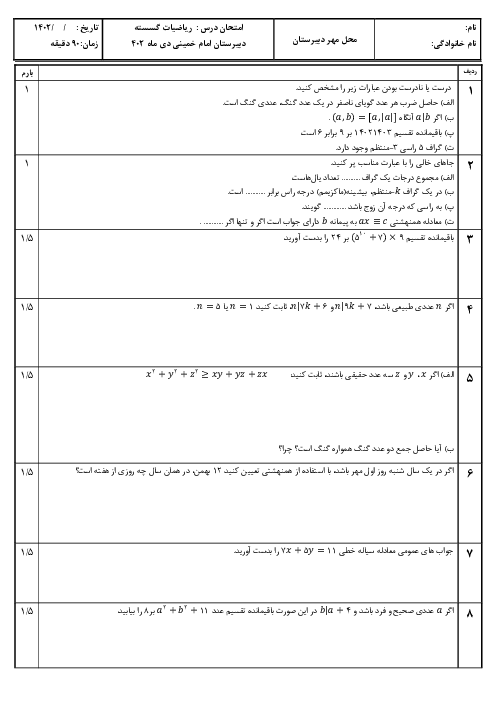
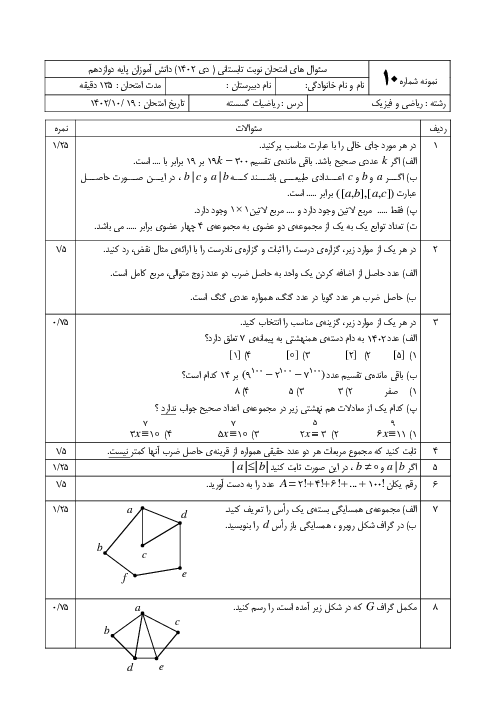
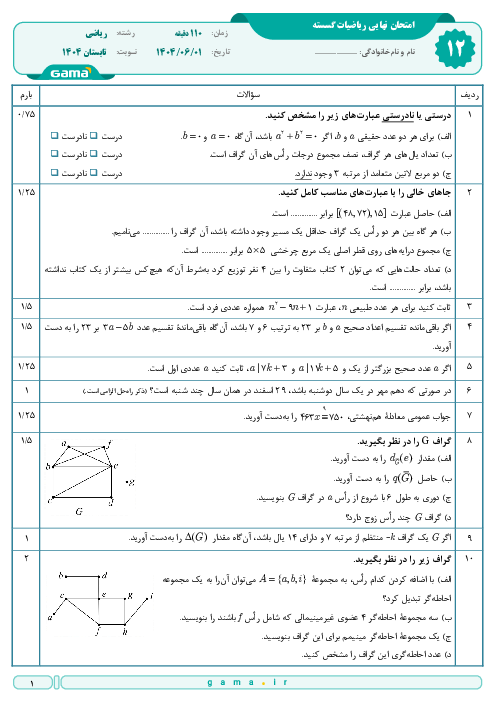
گراف زیر را در نظر بگیرید.
الف) یک مجموعه احاطهگر مینیمال بنویسید که مینیمم نباشد.
ب) یک مجموعه احاطهگر 3 عضوی بنویسید که مینیمال نباشد.
ج) با اضافه کردن حداقل چند یال، عدد احاطهگری این گراف برابر یک میشود؟ دلیل خود را بنویسید.

پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!