آزمون آنلاین هندسه سال دوازدهم | ماتریس و اعمال روی ماتریس‌ها
متوسطه دوم نظری
دوازدهم
علوم ریاضی
هندسه (3)
آبان
شامل مباحث:
درس 1: ماتریس و اعمال روی ماتریس‌ها
تعداد سوالات: 20
سطح دشواری:
متوسط
شروع:
آزاد
پایان:
آزاد
مدت پاسخگویی:
60 دقیقه
رایگان
4,000 تومان
لطفا برای اطمینان از عملکرد و تجربه بهتر از مرورگرهای مدرن و به روز مانند کروم یا فایرفاکس استفاده کنید.
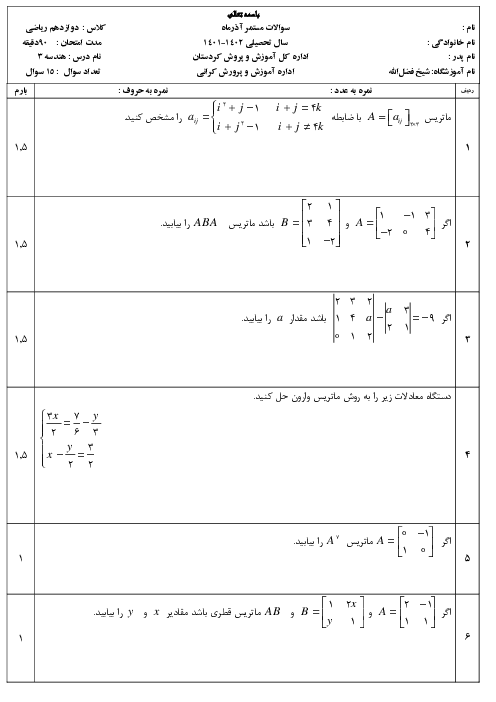
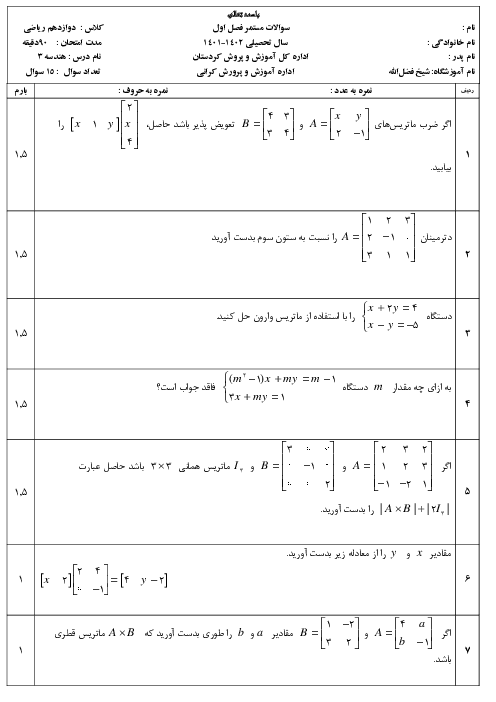
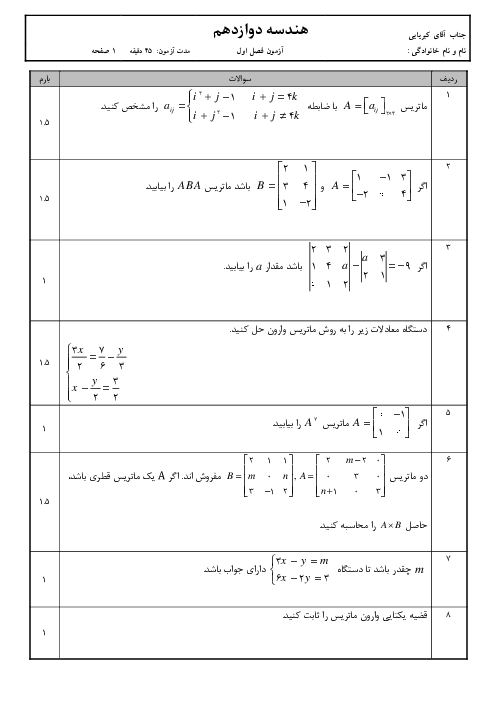
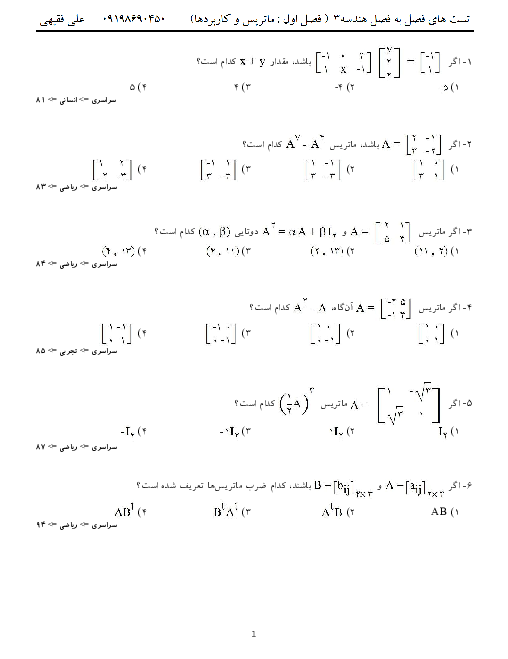
پیش نمایش صفحه اول فایل
آکادمی گاما اگر $C=\left[ \begin{matrix}
3 \\
4 \\
3 \\
\end{matrix}\,\,\,\begin{matrix}
-2 \\
2 \\
1 \\
\end{matrix} \right],B=\left[ \begin{matrix}
2 \\
3 \\
-2 \\
\end{matrix}\,\,\,\begin{matrix}
-1 \\
4 \\
5 \\
\end{matrix} \right],A=\left[ \begin{matrix}
1 \\
5 \\
2 \\
\end{matrix}\,\,\,\begin{matrix}
2 \\
3 \\
1 \\
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...