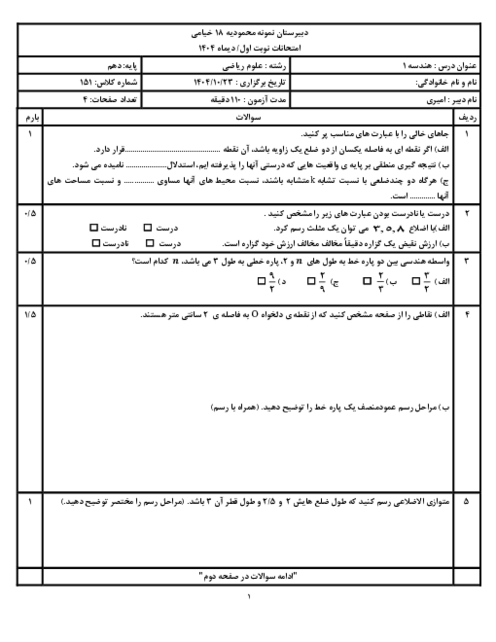
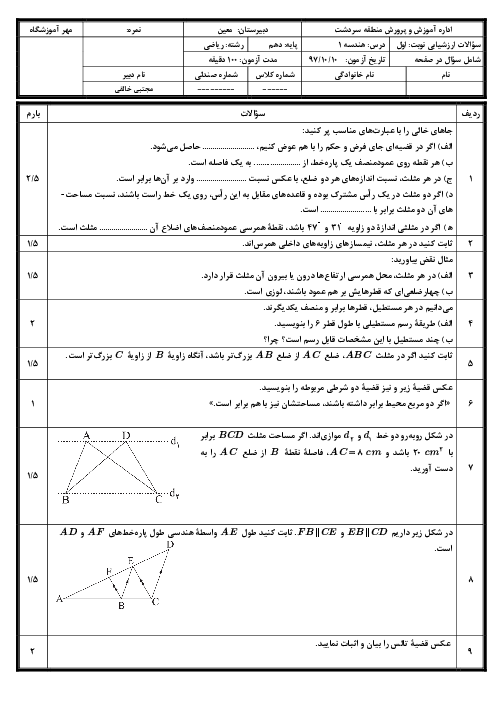
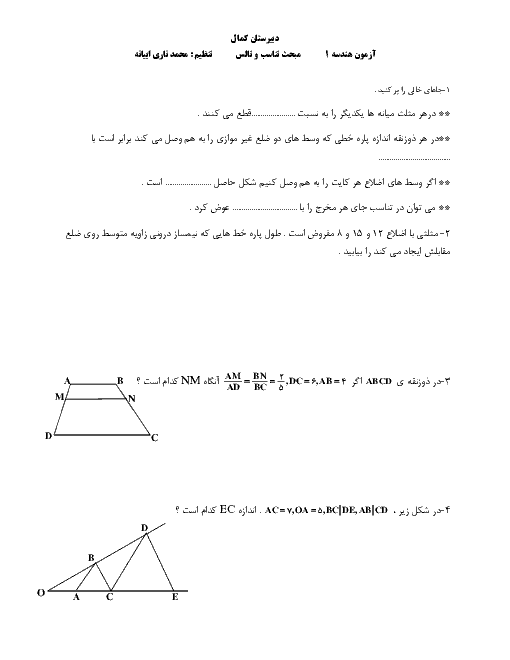
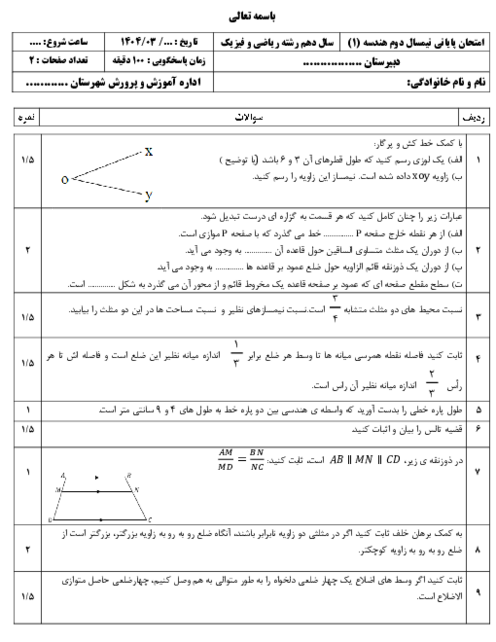
درحال دریافت اطلاعات ...
{{ title }} با پاسخ {{ subtitle }}
-
هندسه (1)
- فصل 1: ترسیمهای هندسی و استدلال
- فصل 2: قضیۀ تالس، تشابه و کاربردهای آن
- فصل 3: چند ضلعیها
- فصل 4: تجسم فضایی