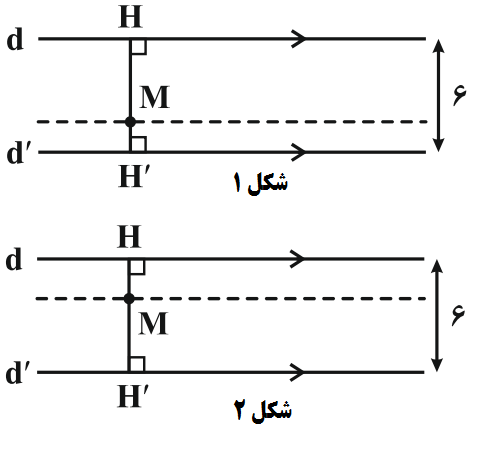
با فرض اینکه نقطهٔ M بین دو خط و نزدیک به خط 'd باشد و با توجه به شکل 1 داریم:
$\begin{matrix}
MH+M{H}'=6 \\
MH-M{H}'=2 \\
\end{matrix}\Rightarrow \left\{ \begin{matrix}
MH=4 \\
M{H}'=2 \\
\end{matrix} \right.$
بنابراین نقاطی که روی خطی موازی دو خط d و 'd و به فاصلهٔ 2 از خط 'd باشند، ویژگی های مسئله را دارا میباشند.
مشابه همین حالت برای زمانی رخ میدهد که نقطه M بین دو خط و این بار نزدیک خط d باشد.
با توجه به شکل 2
$\Rightarrow \left\{ \begin{matrix}
MH=2 \\
M{H}'=4 \\
\end{matrix} \right.$
دقت کنید که اگر نقطهٔ M خارج دو خط باشد، تفاضل فاصلهٔ آن از دو خط، دقیقاً برابر فاصلهٔ بین دو خط بوده و همواره مقداری ثابت است.