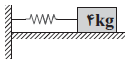
براي به دست آوردن جابه‌جايی جسم می‌بايست مكان نهايی جسم را به دست آوريم، برای اين كار بايد معادله‌ی مكان – زمان نوسانگر را به دست آوريم:

$_{x=A\cos (\omega t)\Rightarrow x=0/2\cos (5\pi t)\xrightarrow{t=0/5s}x=0/2\cos (5\pi \times \frac{1}{2})\Rightarrow x=0/2(\frac{5\pi }{2})=0\Rightarrow \cos (\frac{5\pi }{2})=\cos (2\pi +\frac{\pi }{2})=\cos (\frac{\pi }{2})=0}^{\omega =\sqrt{\frac{k}{m}}\xrightarrow[m=4kg]{k=100{{\pi }^{2}}\frac{N}{M}}\omega =5\pi \frac{rad}{s}}$ 

بنابراين مكان نهايی جسم نقطه‌ی $x=0$ است. پس اندازه‌ی جابه‌جايی جسم $20$ سانتی‌متر می‌شود. برای به دست آوردن مسافت طی شده ابتدا دوره‌ی حركت جسم را به دست می‌آوريم:

$\omega =2\pi f\xrightarrow{\omega =5\pi \frac{rad}{s}}f=2/5Hz\Rightarrow T=\frac{1}{f}\Rightarrow T=\frac{2}{5}s$ 

با توجه به مفهوم دوره‌ی حركت، می‌فهميم كه نوسانگر در يك دوره‌ی حركت، به اندازه‌ی $4A$ يعنی $80$ سانتی‌متر مسافت را طی می‌كند. با توجه به اين‌كه متحرک در لحظه‌ی $t=0/5s$ در مکان $x=0$ قرار دارد، بنابراين مسافت طی شده توسط نوسانگر برابر است با: $l=4A+A=100cm$