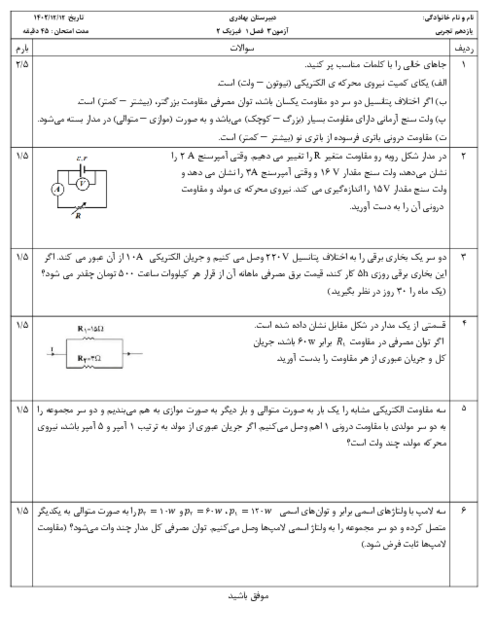
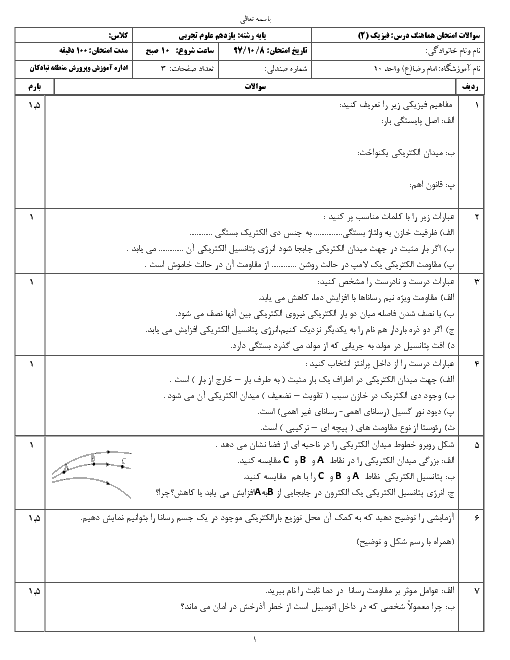
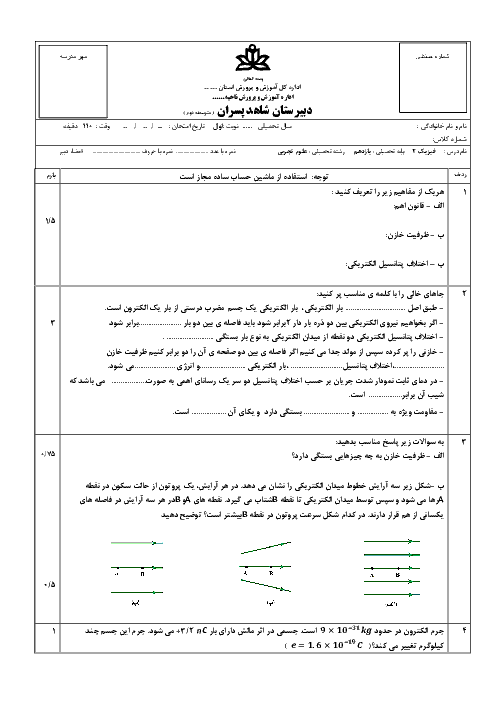
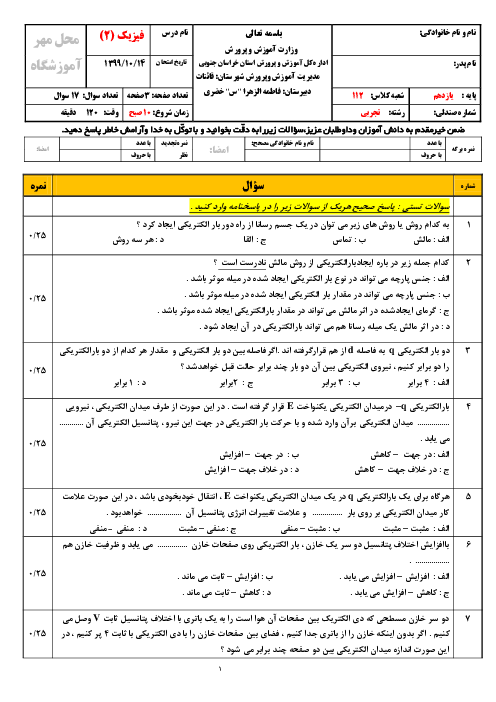
از سیملولهای به ضریب القاوری $0/02$ هانری جریان متناوبی میگذرد که معادلهٔ آن در $SI$ به صورت $I=4\sin (20\pi t)$ است. در لحظهٔ $t=\frac{13}{120}s$ انرژی ذخیره شده در سیملوله چند میلیژول است و تا این مدت چند بار جهت جریان عبوری از سیملوله تغییر کرده است؟
1 )
$40$ ، یک بار
$40$ ، دو بار
3 )
$40\sqrt{3}$ ، یک بار
4 )
$40\sqrt{3}$ ، دو بار
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!