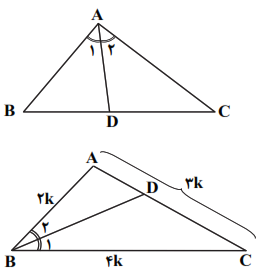
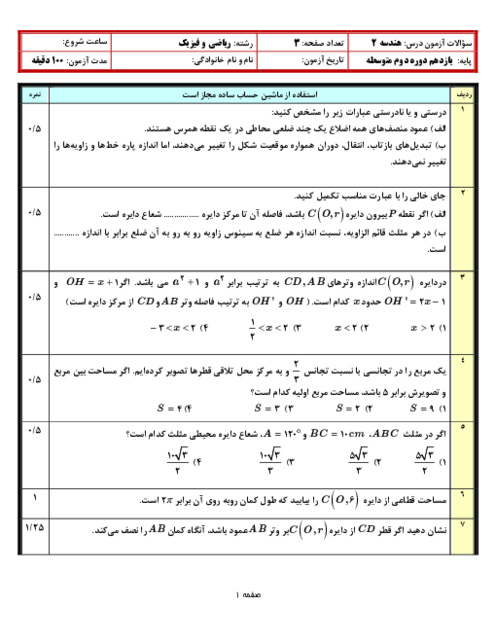
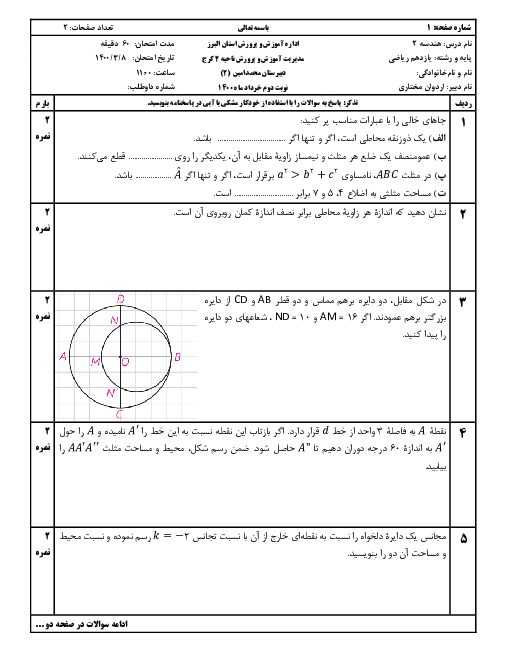
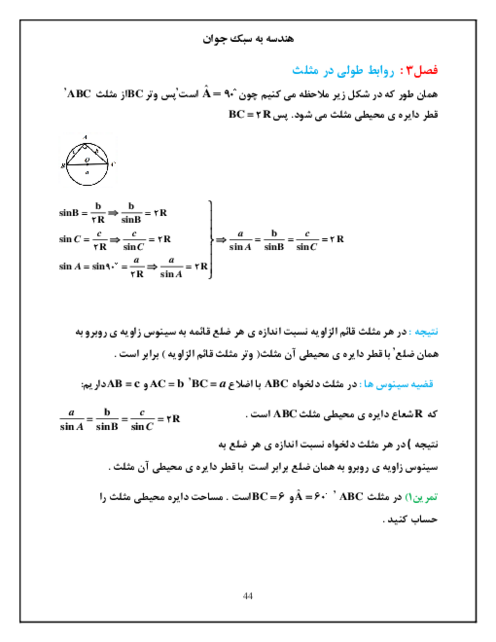
درس 3: قضیۀ نیمسازهای زوایای داخلی و محاسبۀ طول نیمسازها
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اضلاع مثلثی با اعداد 2، 3 و 4 متناسب است و نیمساز زاویهی متوسط، ضلع مقابل را به دو قطعه تقسیم میکند. نسبت این دو قطعه، کدام میتواند باشد؟