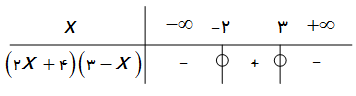در کدام یک از بازههای زیر، تابع $f\left( x \right)=\sqrt{\left( 2x+4 \right)\left( {{x}^{2}}+1 \right)\left( 3-x \right)}$ دارای حد است؟
1 )
$\mathbb{R}$
$\left( -2,3 \right)$
3 )
$\left( 3,2 \right)$
4 )
$\left( -3,-2 \right)\cup \left( 3,4 \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...