درس 2: معادلهٔ درجهٔ دوم و تابع درجه 2
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
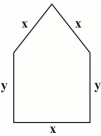
می‌خواهیم پنجره‌ای به شكل مستطیل با یک مثلث متساوی الاضلاع در بالای آن بسازیم. اگر محیط پنجره 6 متر باشد، ابعاد مستطیل چند متر باشد تا پنجره حداكثر نوردهی را داشته باشد؟ ($\frac{\sqrt{3}}{4}$ را 0/5 فرض کنید.)
1 )
$\frac{3}{4}$ و $\frac{3}{5}$
$\frac{3}{2}$ و $\frac{3}{4}$
3 )
$\frac{3}{2}$ و $\frac{2}{5}$
4 )
$\frac{1}{5}$ و $\frac{3}{4}$
پاسخ تشریحی :
تحلیل ویدئویی تست
یوسف شاکر اردکانی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...