درس 3: اعمال جبری روی توابع
ریاضی (2)
یازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
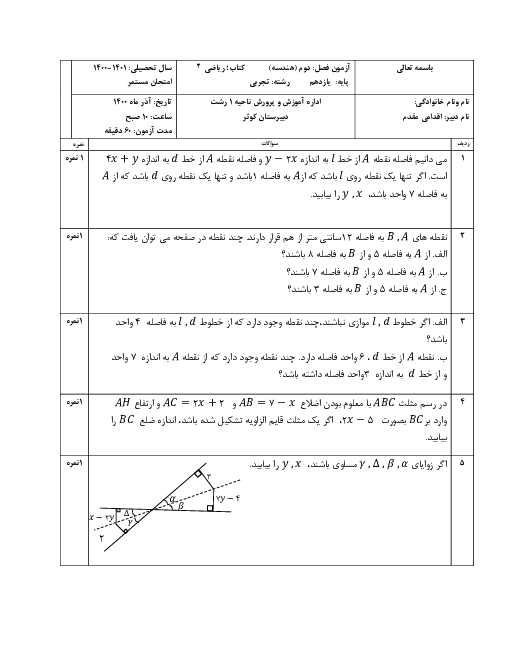
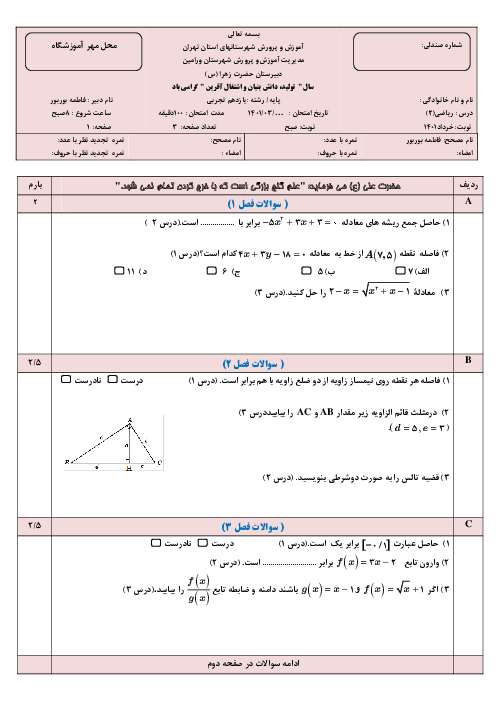
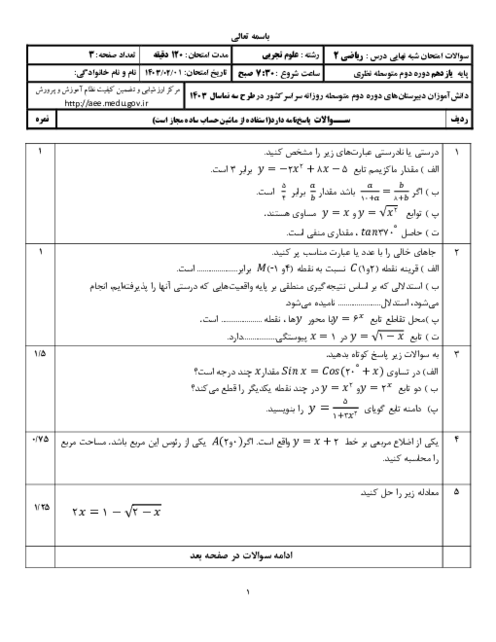
شکل زیر، نمودار تابع $y=f(x+2)$ است. دامنه‌ی تابع $\sqrt{xf(x-1)}$ کدام است؟
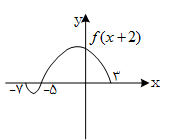
1 )
$\left[ -10,-8 \right]\bigcup \left\{ 0 \right\}$
$\left[ -4,-2 \right]\bigcup \left[ 0,6 \right]$
3 )
$\left[ -7,-5 \right]\bigcup \left[ 0,3 \right]$
4 )
$\left[ -2,6 \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
سعید احمدوند 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...