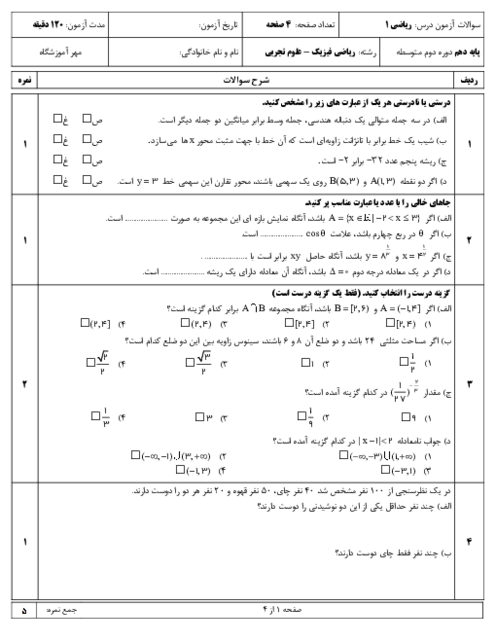
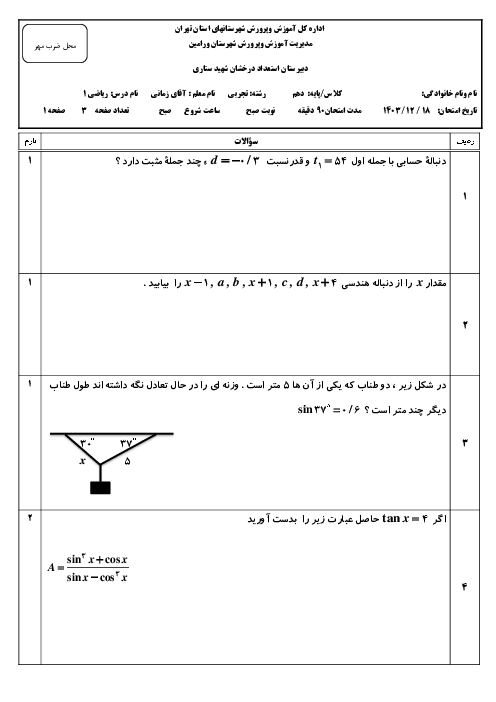
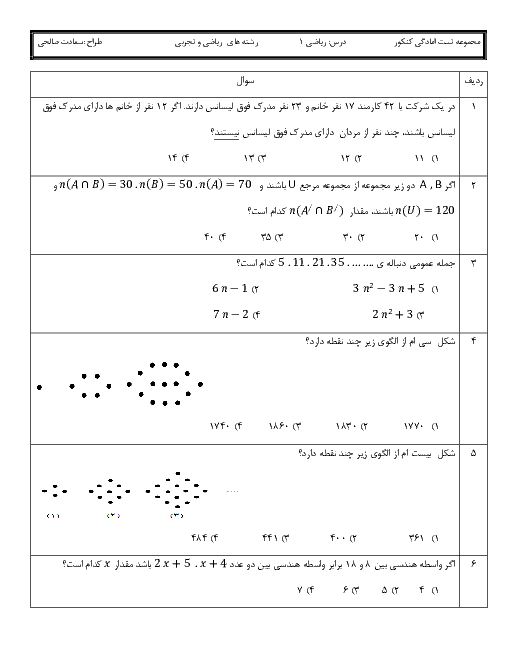
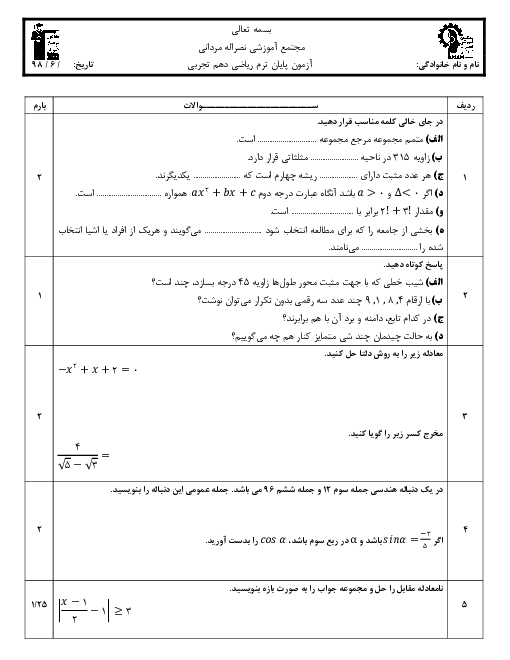
درس 1: مجموعه‌های متناهی و نامتناهی
ریاضی (1)
دهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر $U$ مجموعه‌ی مرجع و $A$ و $B$ دو مجموعه‌ی دلخواه باشند، آنگاه تعداد اعضای کدام گزینه برابر $n(U)-n(A)-n(B)+n(A\bigcap B)$ است؟
1 )
$A \bigcap B'$
2 )
$A' \bigcup B$
$A' \bigcap B'$
4 )
$A' \bigcup B'$
پاسخ تشریحی :
تحلیل ویدئویی تست
ندا تقوی 
حسین زنجانی 
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...