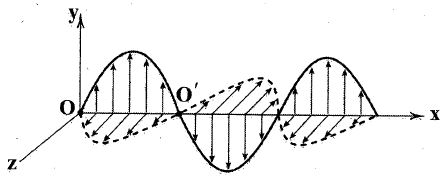
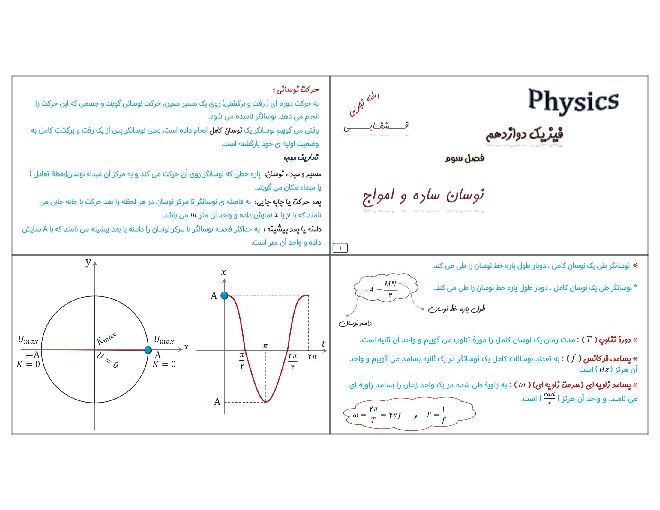
نمودار زیر، تصویر یک موج الکترومغناطیس با بسامد $1/8GHz$ در یک محیط شفاف است. اگر تندی انتشار موج در این محیط برابر $\frac{3}{4}{{({{\mu }_{{}^\circ }}{{\varepsilon }_{{}^\circ }})}^{-\frac{1}{2}}}$ باشد، فاصله‌ی بین نقاط $O$ و ${O}'$ برابر چند متر است؟
($:{{\mu }_{{}^\circ }},c=3\times {{10}^{8}}\frac{m}{s}$ ضریب تراوایی مغناطیسی و $:{{\varepsilon }_{{}^\circ }}$ ضریب گذردهی خلا)
تحلیل ویدئویی تست
محسن ذوالفقاری 
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...