درس 3: چند ضلعی‌های محاطی و محیطی
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
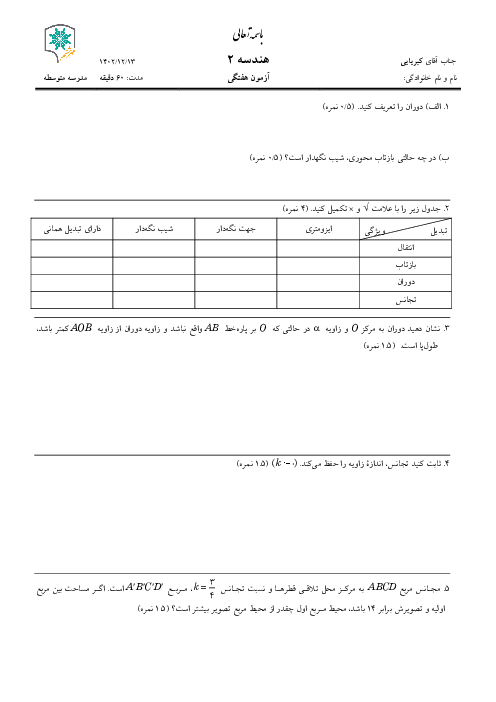
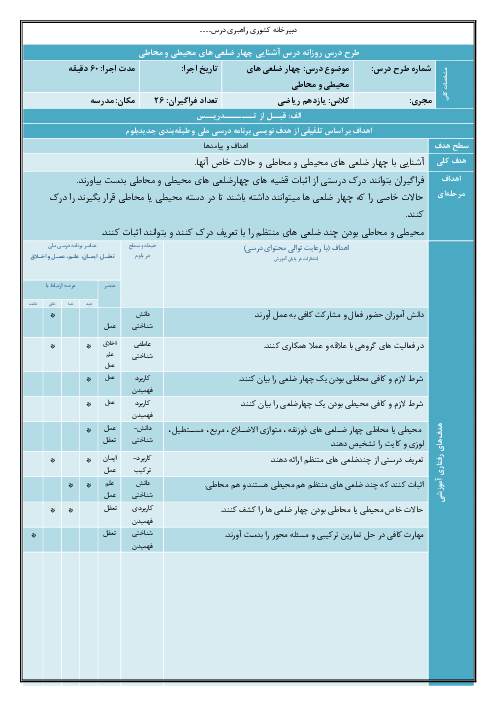
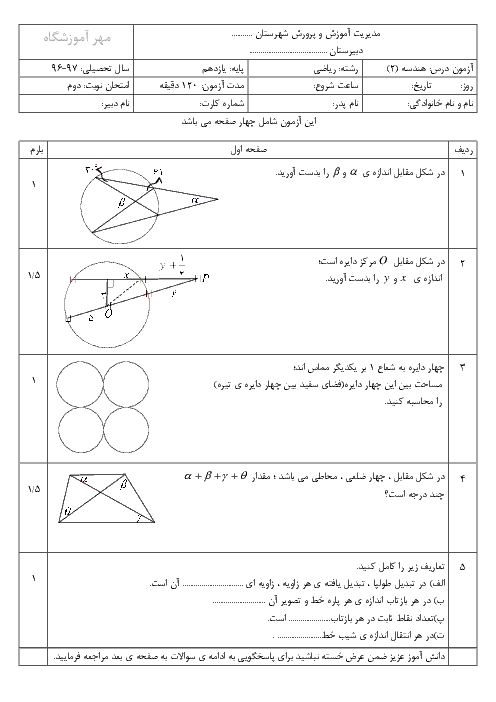
اگر اضلاع مثلث $ABC$ را $a$، $b$ و $c$ و شعاع دايره‌های محاطی خارجی متناظر با اين اضلاع را به‌ترتيب ${{r}_{a}}$، ${{r}_{b}}$ و ${{r}_{c}}$ بنامیم و داشته باشیم: $a\gt b\gt c$، آن‌گاه كدام گزينه همواره صحيح است؟
1 )
${{r}_{a}}\lt {{r}_{b}}\lt {{r}_{c}}$
2 )
${{r}_{b}}\gt {{r}_{a}}\gt {{r}_{c}}$
3 )
${{r}_{b}}\lt {{r}_{c}}\lt {{r}_{a}}$
${{r}_{a}}\gt {{r}_{b}}\gt {{r}_{c}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...