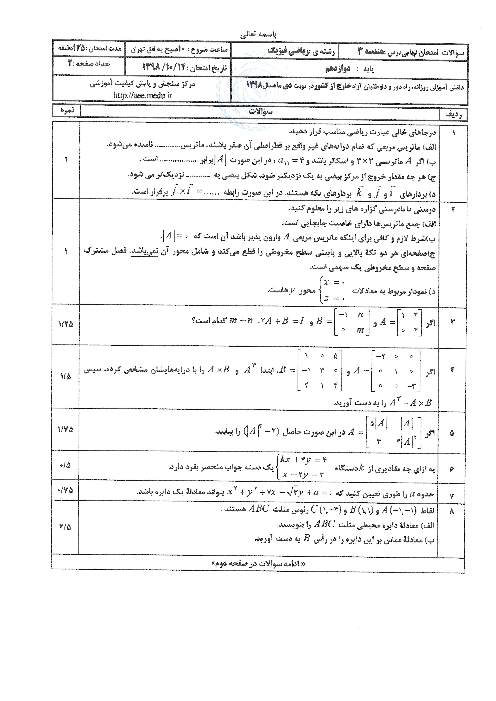
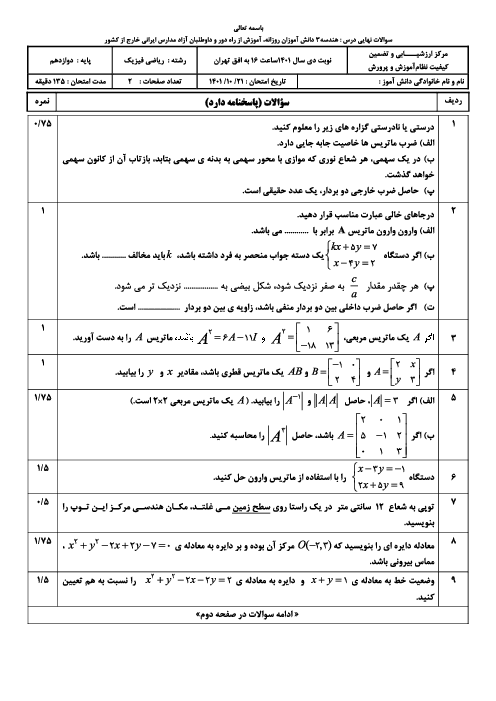
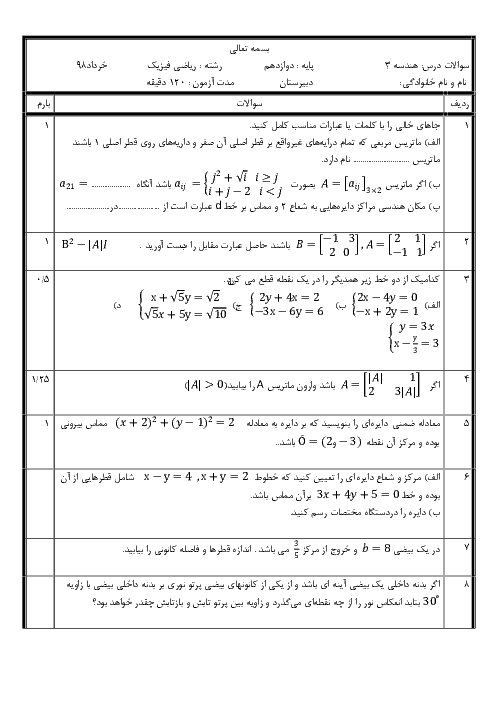
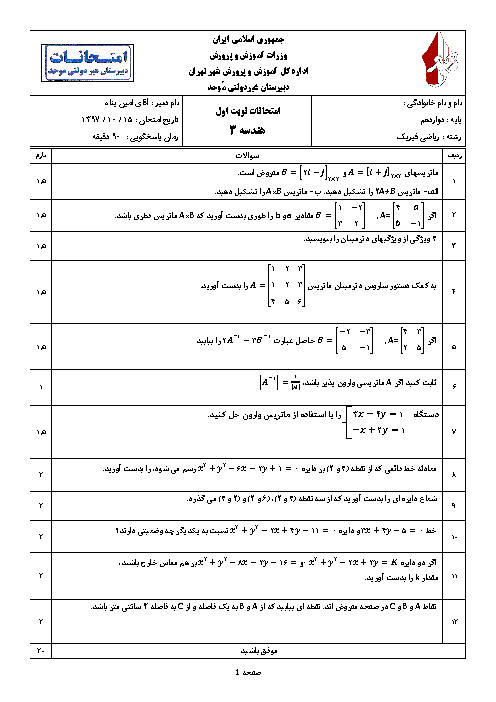
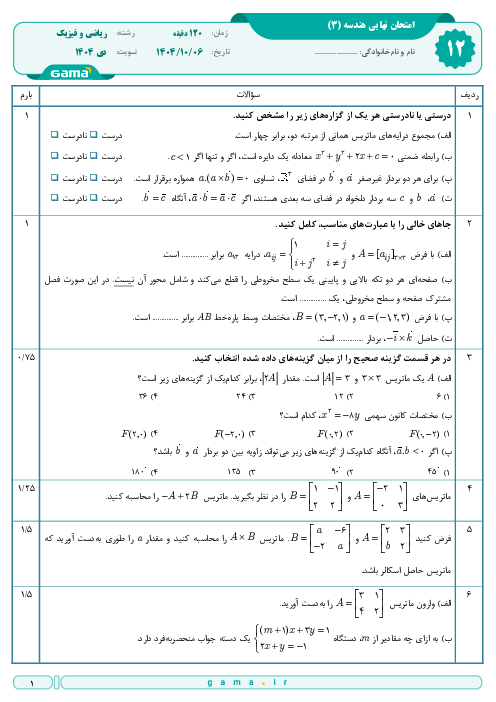
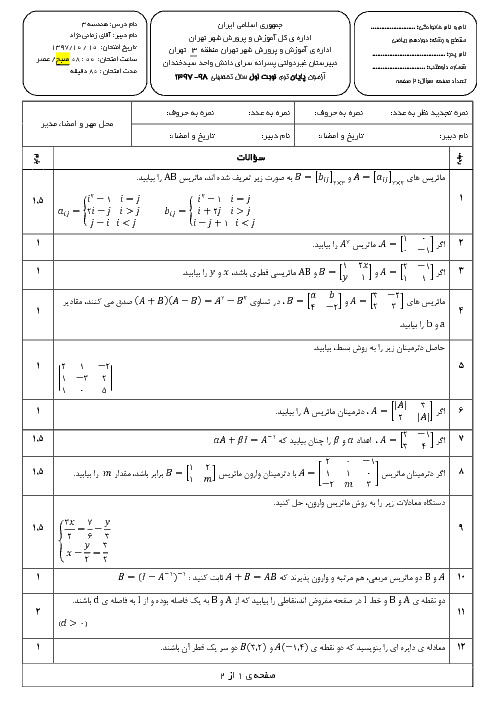
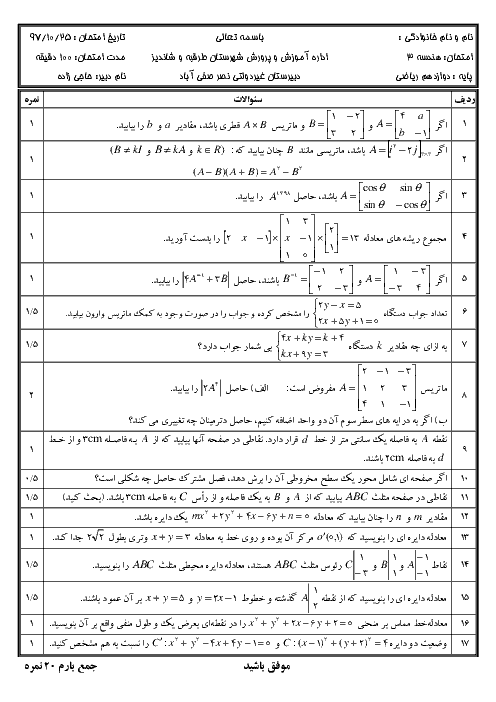
فرم معتبر نیست.
مقدار m را چنان تعیین کنید که دایره به معادله ${x^2} + {y^2} + 2x - 2y + m = 0$ با دایره به مرکز $O(2\,,\, - 3)$ و شعاع 3 مماس بیرون باشد.
پاسخ تشریحی :
نمایش پاسخ
$O(2\,,\, - 3)\;,\;r = 3$
$O'( - 1\,,1)\;,\;r' = \frac{1}{2}\sqrt {8 - 4m} = \sqrt {2 - m} $
$d = OO' = \sqrt {9 + 16} = 5r + r' = d \Rightarrow 3 + \sqrt {2 - m} = 5$
$\Rightarrow \sqrt {2 - m} = 2 \Rightarrow 2 - m = 4 \Rightarrow m = -2$
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...