گاما رو نصب کن!
گاما رو نصب کن!
به پاس اعتمادی که به گاما داشتی، ما به طور ویژه «بسته یک‌ساله گاما» رو برات فعال کردیم تا بدون هیچ نگرانی از محدودیت زمانی، از سرویس‌های ویژه گاما استفاده کنی.
اگه به اطلاعات بیشتری نیاز داری راهنمای تغییرات جدید رو ببین.
از همراهیت با گاما سپاسگزاریم.
با تقدیم احترام
پربازدیدها: #{{ tag.title }}
با سپاس! گزارش شما ثبت شد.
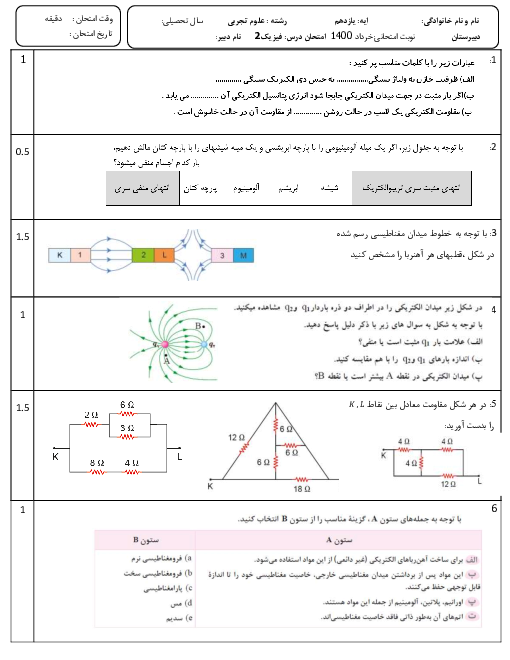
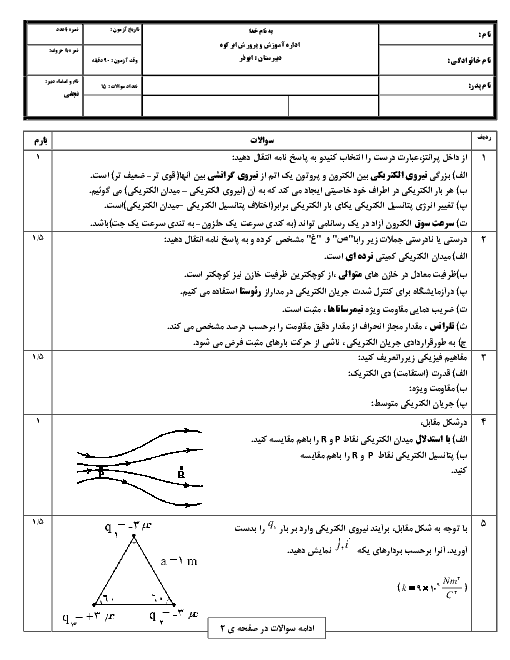
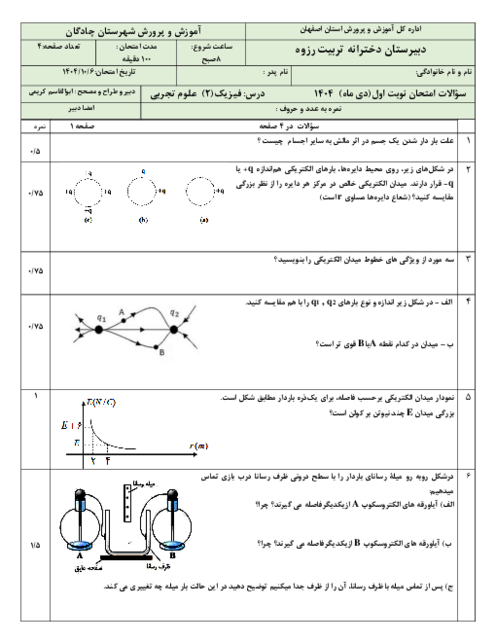
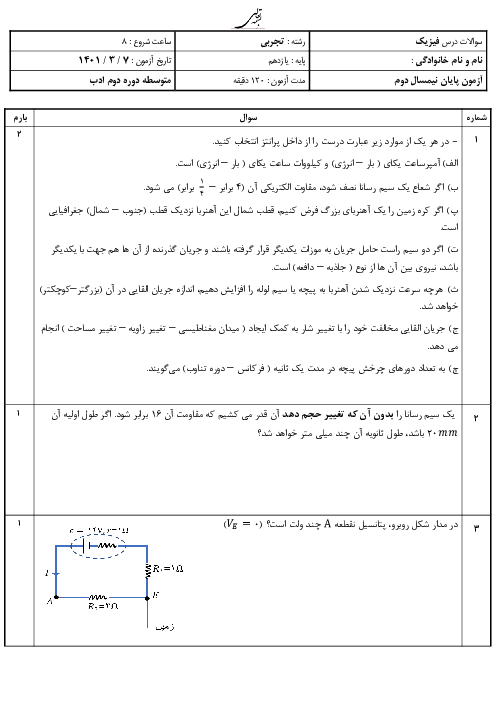
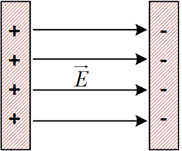
مطابق شکل زیر، دو صفحهٔ رسانا با بارهای هم‌اندازه و ناهم‌نام در فاصلهٔ 5 سانتی‌متری از یکدیگر قرار گرفته‌اند و میدان الکتریکی یکنواخت $\overrightarrow{E}$ به بزرگی $10\frac{kN}{C}$ بین دو صفحه ایجاد شده است. اگر پروتونی را از کنار صفحهٔ با بار مثبت رها کنیم، تندی آن هنگامی که به صفحهٔ با بار منفی میرسد، چند متر بر ثانیه است؟ (بار پروتون ${{e}_{p}}=1/6\times {{10}^{-19}}C$، جرم پروتون ${{m}_{p}}=2\times {{10}^{-27}}kg$ و از نیروی وزن وارد بر پروتون و اصطکاک صرف‌نظر شود.)
1 )
$2\times {{10}^{5}}$
$2\sqrt{2}\times {{10}^{5}}$
3 )
$4\times {{10}^{5}}$
4 )
$4\sqrt{2}\times {{10}^{5}}$
محسن ذوالفقاری 
