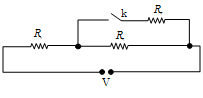
قبل از بستن كليد $k$، مقاومت ${{R}_{3}}$ در مدار نیست و مدار فقط شامل مقاومت‌های متوالی ${{R}_{1}}$ و ${{R}_{2}}$ است. از طرفی چون مقاومت‌ها مشابه‌اند، ولتاژ $V$  به طور مساوی بين آن‌ها تقسيم می‌شود، بنابراين برای مقاومت ${{R}_{1}}$ داریم:

${{P}_{1}}=\frac{V_{1}^{2}}{{{R}_{1}}}\xrightarrow[{{R}_{1}}=R]{{{V}_{1}}=\frac{V}{2}}{{P}_{1}}=\frac{{{(\frac{V}{2})}^{2}}}{R}\Rightarrow {{P}_{1}}=\frac{1}{4}\times \frac{{{V}^{2}}}{R}$

از بستن كليد $k$، مقاومت‌های ${{R}_{3}}$ و ${{R}_{2}}$ با هم موازی‌اند و چون مشابه‌اند، مقاومت معادل آن‌ها ${{R}_{2,3}}=\frac{R}{2}$ می‌شود که این مقاومت به طور متوالی با مقاومت ${{R}_{1}}$ قرار می‌گیرد.

در اين حالت طبق رابطهٔ $V=RI$، ولتاژ $V$ به نسبت 2 به 1 بين مقاومت‌ها تقسيم می‌شود (يعنی $V$ به 3 قسمت مساوی تقسيم می‌شود) كه به مقاومت بزرگ‌تر (يعنی 1 يعنی ${{R}_{1}}=R$) دو قسمت از 3 قسمت می‌رسد یعنی ${{V}_{1}}^{\prime }=\frac{2}{3}V$ می‌شود. در اين حالت برای مقاومت ${{R}_{1}}$ داريم:

${{P}_{1}}^{\prime }=\frac{{{V}_{1}}{{^{\prime }}^{2}}}{{{R}_{1}}}\xrightarrow[{{R}_{1}}=R]{{{V}_{1}}^{\prime }=\frac{2}{3}V}{{P}_{1}}^{\prime }=\frac{4}{9}\frac{{{V}^{2}}}{R}$ 

در نهایت داریم:

$\frac{{{P}_{1}}^{\prime }}{{{P}_{1}}}=\frac{\frac{4}{9}\frac{{{V}^{2}}}{R}}{\frac{1}{4}\frac{{{V}^{2}}}{R}}\Rightarrow \frac{{{P}_{1}}^{\prime }}{{{P}_{1}}}=\frac{16}{9}$