گام اول: حرکت اتومبیل شامل دو بخش است. بخش اول از لحظهٔ دیدن مانع تا لحظهٔ ترمز گرفتن (مدت‌زمان واکنش) و بخش دوم از لحظهٔ ترمزگرفتن تا توقف.
مسافت طی‌شده توسط اتومبیل در این دو بخش را به دست می‌آوریم. در بخش اول اتومبیل با سرعت ثابت در حال حرکت است؛ بنابراین:

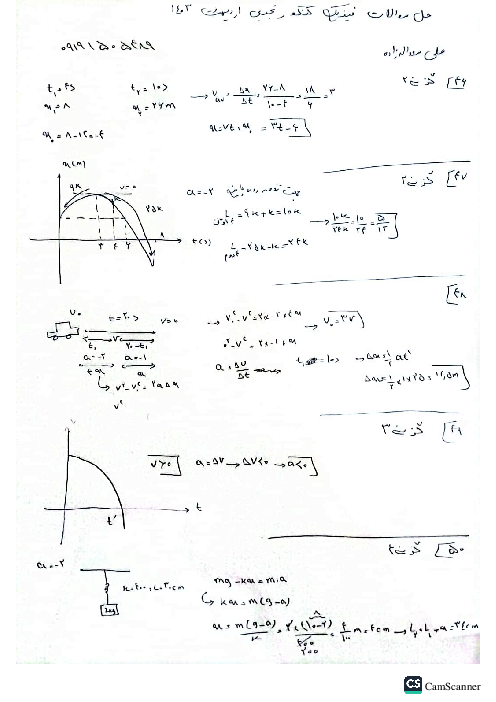
${x_1} = {v_1}{t_1} \to {v_1} = 72km/h = 20m/s\backslash {t_1} = 0/5s \to {x_1} = 20 \times 0/5 = 10m$

در بخش دوم، اتومبیل با شتاب ثابت $a =  - 4m/{s^2}$، شروع به توقف می‌کند؛ بنابراین:

$v_2^2 - v_1^2 = 2a\Delta x \Rightarrow {0^2} - {(20)^2} = 2 \times ( - 4) \times \Delta x$

$ \Rightarrow \Delta x = 50m$

جابه‌جایی کل اتومبیل تا لحظهٔ توقف برابر $10 + 50 = 60m$ به دست آمد. چون فاصلهٔ اولیهٔ اتومبیل تا مانع $52m$ بود، اتومبیل به مانع برخورد خواهد کرد. (رد گزینه‌های 1 و 2)

گام دوم: اتومبیل قبل از ترمزکردن مسافت $10m$ را می‌پیماید. بنابراین برای تعیین تندی برخورد آن به مانع، $52 - 10 = 42m$ پایانی حرکت را بررسی می‌کنیم:

${v'^2} - v_1^2 = 2a\Delta x' \Rightarrow {v'^2} - {(20)^2} = 2 \times ( - 4) \times 42$
$ \Rightarrow {v'^2} = 64 \Rightarrow v' = 8m/s$