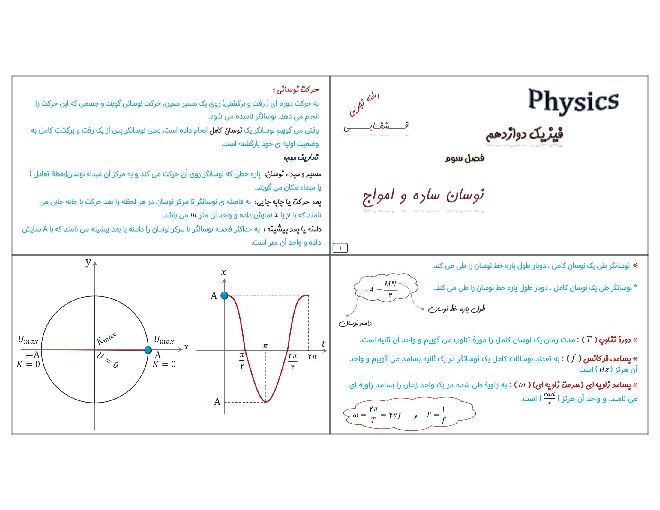
از روی نمودار مشخص است که جهت حرکت متحرک در لحظهٔ $t = 2s$ تغییر کرده است؛ بنابراین اگر $t = 2s$ لحظهٔ وسط بازهٔ زمانی $({t_1},{t_2})$ باشد، مکان متحرک در لحظات ${t_1}$ و ${t_2}$ یکسان است. در نتیجه مطابق شکل مقابل مکان متحرک در لحظات صفر و $4s$ و هم‌چنین $1s$ و $3s$ یکسان است.

حالا به بررسی گزینه‌ها می‌پردازیم:

1- نادرست؛ می‌دانیم تندی متحرک در اطراف نقطهٔ تغییر جهت، کم‌تر از سایر نقاط است. بنابراین می‌توان گفت در بازه‌های زمانی یکسان، مسافت طی‌شده توسط متحرک در اطراف نقطهٔ تغییر جهت، کم‌تر از نقاط دیگر است. با توجه به این موضوع چون لحظهٔ $t = 2s$ در 3 ثانیهٔ اول قرار دارد، می‌توان نتیجه گرفت که مسافت طی‌شده توسط متحرک در 3 ثانیهٔ اول کمتر از مسافت طی‌شده در 3 ثانیهٔ دوم است.

2- نادرست؛ در 3 ثانیهٔ اول یعنی بازهٔ زمانی $(0,3s)$ متحرک تغییر جهت می‌دهد (لحظهٔ $t = 2s$) بنابراین در این بازهٔ زمانی مسافت طی‌شده توسط متحرک با اندازهٔ جابه‌جایی آن برابر نیست.

3- نادرست؛ مکان متحرک در لحظات صفر و $4s$ یکسان است. بنابراین سرعت متوسط متحرک در 4 ثانیهٔ اول حرکت برابر صفر است. از طرفی از روی نمودار مشخص است که سرعت متوسط متحرک در بازهٔ زمانی $(1s,5s)$ برابر صفر نیست.

4- درست؛ متحرک در 3 ثانیهٔ اول حرکت از مکان ${x_0}$ به ${x_1}$ و در بازهٔ زمانی $(1s,4s)$ از مکان ${x_1}$ به ${x_0}$ رفته است. بنابراین اندازهٔ جابه‌جایی متحرک در این دو بازهٔ زمانی برابر است و می‌توان گفت:

$\left| {\Delta {x_{(0,3s)}}} \right| = \Delta {x_{(1s,4s)}} = {x_0} - {x_1}$
$ \Rightarrow \frac{{\left| {\Delta {x_{(0,3s)}}} \right|}}{{3 - 0}} = \frac{{\Delta {x_{(1s,4s)}}}}{{4 - 1}} \Rightarrow \left| {{v_{av(0,3s)}}} \right| = {v_{av(1s,4s)}}$