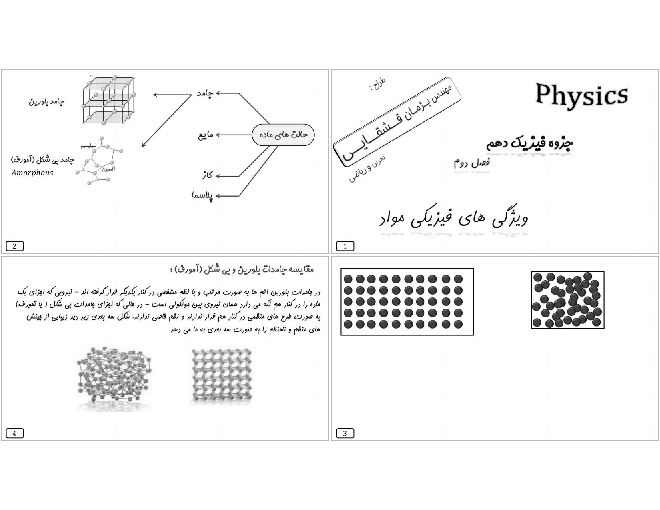
گام اول: مطابق شکل نقطهٔ رهاکردن گلوله را نقطهٔ (1) و نقطهٔ برخورد به سطح زمین را نقطهٔ (2) در نظر گرفته و اصل پایستگی انرژی مکانیکی را برای این دو نقطه مینویسیم (سطح زمین به عنوان مبدأ پتانسیل گرانشی در نظر گرفته شده است):

${E_1} = {E_2} \Rightarrow {K_1} + {U_1} = {K_2} + {U_2}$

${K_1} = {U_2} = 0 \to mg{h_1} = \frac{1}{2}mv_2^2 \Rightarrow v_2^2 = 2 \times 10 \times 45$

$ \Rightarrow {v_2} = 30m/s$

گام دوم: مطابق شکل ارتفاع بیشینه‌ای که گلوله پس از برخورد به سطح زمین، به آن می‌رسد را نقطهٔ (3) در نظر گرفته و اصل پایستگی انرژی مکانیکی را برای نقاط (2) و (3) می‌نویسیم.

${E'_2} = {E_3} \Rightarrow {K'_2} + {U_2} = {K_3} + {U_3}$
${U_2} = {K_3} = 0 \to \frac{1}{2}mv'_2^2 = mg{h_3} \Rightarrow v'_2^2 = 2 \times 10 \times 20$
$ \Rightarrow v' = 20m/s$

گام سوم: گلوله با سرعت $30m/s$ به سطح زمین برخورد کرده و با سرعت $20m/s$ از سطح زمین برمی‌گردد؛ بنابراین با در نظر گرفتن جهت مثبت به سمت بالا بزرگی تغییر تکانهٔ گلوله در این مدت به صورت زیر به دست می‌آید:

$\Delta p = \left| {{{p'}_2} - {p_2}} \right| = \left| {m{{v'}_2} - m{v_2}} \right|$
$ = \left| {0/2 \times 20 - 0/2 \times ( - 30)} \right|$
$ \Rightarrow \Delta p = \left| {4 + 6} \right| = 10\frac{{kg.m}}{s}$

گام چهارم: بزرگی نیروی خالص متوسط وارد بر گلوله در این مدت برابر است با:

$\left| {{F_{av}}} \right| = \frac{{\left| {\Delta p} \right|}}{{\Delta t}} = \frac{{10}}{{2 \times {{10}^{ - 3}}}} = 5000N$