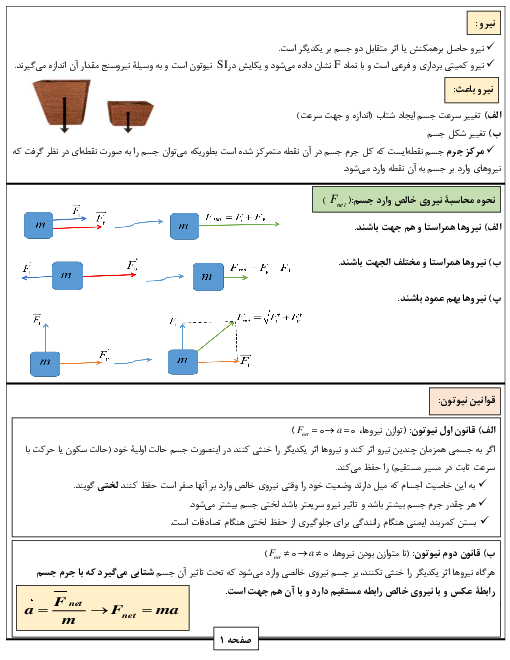
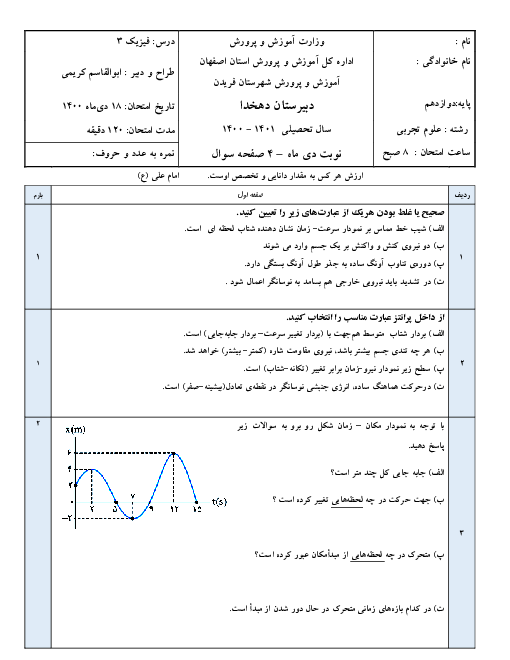
نیروی خالص F به وزنهای به جرم m شتابی به بزرگی aمتر بر مجذور ثانیه میدهد. اگر جرم وزنه را نصف کنیم و اندازۀ نیرو را بدون تغییر جهت 25 درصد افزایش دهیم، بزرگی شتاب جسم $a+\frac{3}{2}$متر بر مجذور ثانیه خواهد شد. شتاب وزنه در حالت دوم چند $\frac{m}{{{s}^{2}}}$ است؟