نكته: در تابع $f$، مجموعه نقاط شامل نقاطی كه مشتقِ تابع در آن‌ها وجود ندارد و نقاطی كه مشتق در آن‌ها برابر صفر است را نقاط بحرانی $f$ می‌ناميم.

نكته: برای يافتن اكسترمم مطلق يک تابع كافی است ابتدا مقادير تابع را در نقاط بحرانی و نقاط ابتدا و انتهای بازه به‌دست آوريم. نقطه يا نقاطی كه بيش‌ترين مقدار تابع در آن‌ها اتفاق می‌افتد نقاط ماكزيمم مطلق تابع و مقدار تابع در اين نقاط مقدار ماكزيمم مطلق تابع است. همچنين در بين نقاط مذكور نقطه يا نقاطی كه كم‌ترين مقدار تابع در آن‌ها اتفاق می‌افتد نقاط مينيمم مطلق تابع و مقدار تابع در اين نقاط مقدار مينيمم مطلق تابع است. 

نكته: اگر $O(0,0)$ مركز دايره به شعاع $R$ باشد، معادلۀ دايره ${{x}^{2}}+{{y}^{2}}={{R}^{2}}$ است.

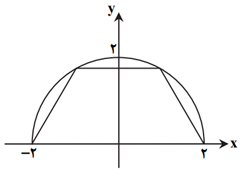
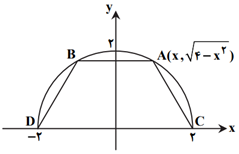
شعاع دايره ۲ و مركز آن مبدأ مختصات است، پس معادلۀ آن به‌صورت ${{x}^{2}}+{{y}^{2}}=4$ است. و ضابطۀ نيم‌دايرهٔ داده‌شده به‌صورت $y=\sqrt{4-{{x}^{2}}}$ می‌باشد.

$S$ ذوزنقه $=\frac{AB+CD}{2}\times {{y}_{A}}=(\frac{2x+4}{2})\sqrt{4-{{x}^{2}}}=(x+2)\sqrt{4-{{x}^{2}}}$

برای بيش‌ترين مقدار مساحت بايد ماكزيمم مطلق تابع را به‌دست آوريم. برای اين‌كار نقاط بحرانی را به‌دست می‌آوريم. به‌كمک مشتق تابع مساحت داريم: 

${S}'=\sqrt{4-{{x}^{2}}}-\frac{2x}{2\sqrt{4-{{x}^{2}}}}(x+2)=0\Rightarrow {S}'(x)=\frac{4-{{x}^{2}}-x(x+2)}{\sqrt{4-{{x}^{2}}}}=0$

$\Rightarrow 4-{{x}^{2}}-{{x}^{2}}-2x=0\Rightarrow {{x}^{2}}+x-2=0\Rightarrow \left\{ \begin{matrix} x=1  \\ x=-2  \\ \end{matrix} \right.$ غ‌ق‌ق

حال مقادیر تابع را به‌ازای $x=1$، $x=2$ و $x=-2$ به‌دست می‌آوریم.

$S(1)=3\sqrt{3},S(2)=S(-2)=0$

بنابراين بيش‌ترين مقدار مساحت برابر $3\sqrt{3}$ است.