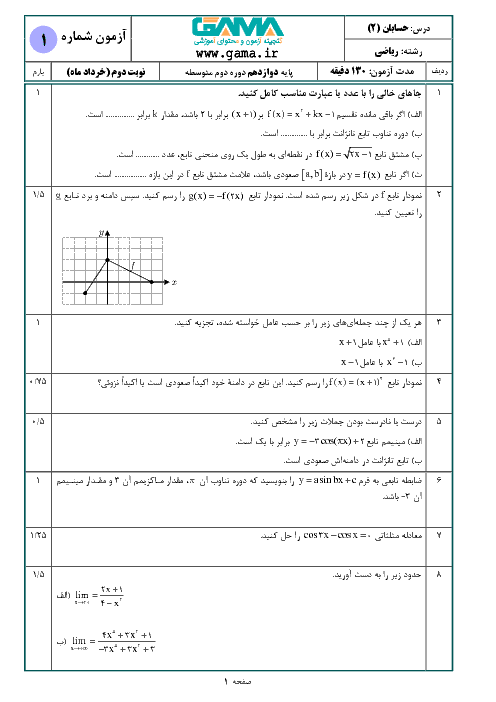
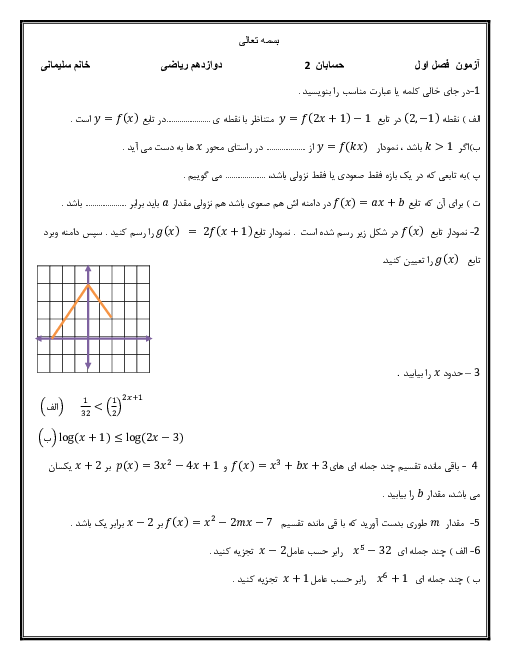
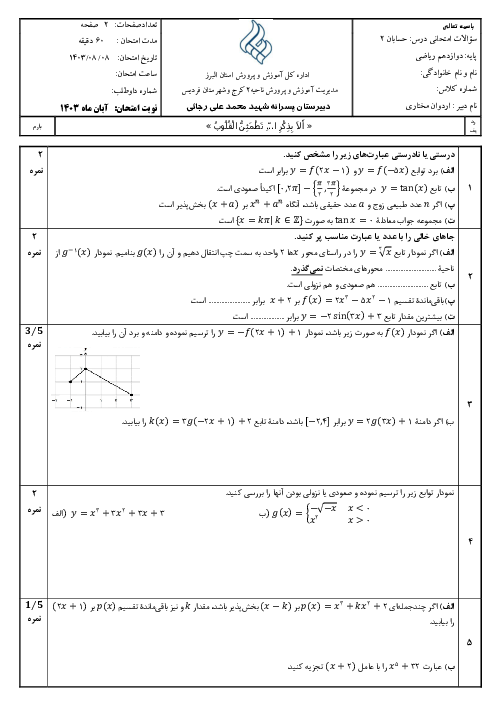
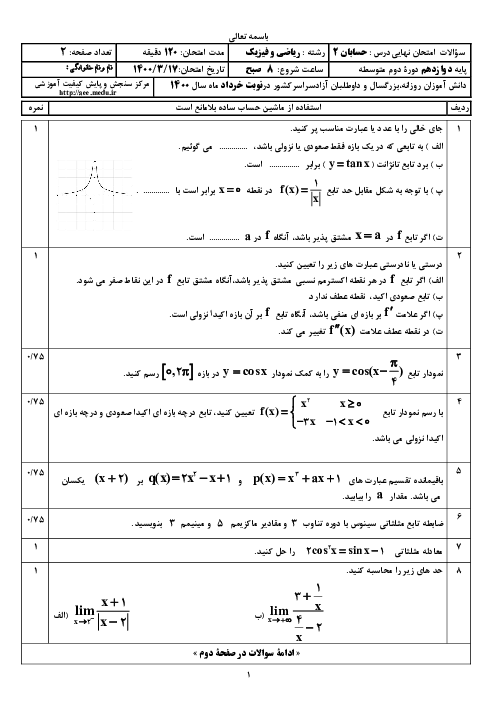
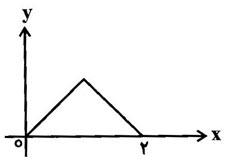
اگر نمودار تابع $f$ به شکل زیر باشد، دامنهی تابع $g$ با ضابطهی $g\left( x \right)=\frac{f\left( 1-x \right)}{f\left( x \right)}$ کدام است؟
1 )
$\left( -1,1 \right)-\left\{ \left. 0 \right\} \right.$
2 )
$\left[ 0,\frac{\sqrt{2}}{2} \right)$
3 )
$\left[ -1,1 \right]-\left\{ \left. 0 \right\} \right.$
$\left( 0,1 \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...