درس 1: توابع چند جمله‌ای- توابع صعودی و نزولی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
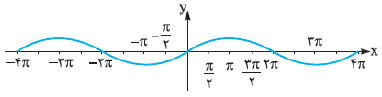
در تابع $y=\sin \frac{x}{2}$ در کدام بازه با افزایش طول نقاط، مقدار تابع کاهش نمی‌یابد؟
1 )
$\left[ -\frac{\pi }{2},\frac{3\pi }{2} \right]$
$\left[ -\frac{\pi }{4},\frac{3\pi }{4} \right]$
3 )
$\left[ \frac{3\pi }{2},\frac{5\pi }{2} \right]$
4 )
$\left[ \pi ,\frac{5\pi }{2} \right]$
پاسخ تشریحی :
تحلیل ویدئویی تست
مهدی خلجی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...