نكته: تابع ثابت، تنها تابعی است كه هم صعودی و هم نزولی است.
هريک از گزينهها را بررسی میكنيم:
گزینهٔ 1: تابع $f(x)=\left[ x \right]$ تابعی صعودی است. نادرست
گزینهٔ 2: تابع را بهصورت $f(x)=\left[ x \right]+1+\left[ x \right]-1=2\left[ x \right]$ میتوان ساده کرد که مانند گزینهٔ 1 تابعی صعودی است. نادرست
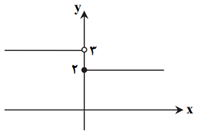
گزينۀ ۳: بيانگر تابعی نزولی است. (به نمودار تابع توجه كنيد.) نادرست
گزينۀ ۴: تابعی ثابت است؛ زيرا:
$f(x)=\left[ x \right]-\left[ x+2 \right]=\left[ x \right]-(\left[ x \right]+2)=\left[ x \right]-\left[ x \right]-2=-2$
بنابراين اين تابع هم صعودی و هم نزولی است. درست