درس 2: رابطه‌های طولی در دایره
هندسه (2)
یازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
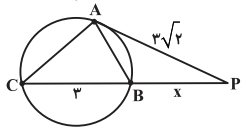
از نقطهٔ P در خارج دایره‌ای، مماس PA به طول $3\sqrt{2}$ را بر آن رسم كرده‌ايم (A روی دايره است). همچنين خط راستی از P گذرانده‌ايم كه دايره را در دو نقطهٔ B و C قطع كرده و $BC=3$ (Bبین P و C) است.نسبت $\frac{AC}{AB}$ کدام است؟
1 )
$\frac{\sqrt{2}}{2}$
2 )
$\frac{\sqrt{3}}{3}$
$\sqrt{2}$
4 )
$\sqrt{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...