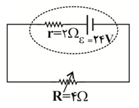
راه حل اول: در حالت اول ابتدا جريان عبوری از مدار را به‌صورت زير محاسبه می‌كنيم:

$I=\frac{\varepsilon }{r+R}\Rightarrow I=\frac{24}{4+2}=4A$

در اين حالت اختلاف پتانسيل دو سر مولد برابر است با: 

${{V}_{a}}-{{V}_{b}}=\varepsilon -rI\Rightarrow {{V}_{a}}-{{V}_{b}}=24-2\times 4=16V$

در نتیجه توان خروجی مولد برابر است با: 

$P=VI=16\times 4=64W$

حال جريان ديگری كه سبب می‌شود توان خروجی مولد 64 وات باقی بماند را محاسبه می‌كنيم. 

${P}'={V}'{I}'\Rightarrow {V}'{I}'=\varepsilon {I}'-r{{{I}'}^{2}}\Rightarrow 64=24{I}'-2{{{I}'}^{2}}$

$\Rightarrow {I}'=4A,{I}'=8A$

مقاومت در اين حالت برابر است با: 

${I}'=\frac{\varepsilon }{r+{R}'}\Rightarrow 8=\frac{24}{2+{R}'}\Rightarrow {R}'=1\Omega $

$\frac{\Delta R}{R}\times 100=\frac{1-4}{4}\times 100=-75$ درصد

راه حل دوم: توان خروجی مولد به ازای مقاومت ${{R}_{1}}$ و ${{R}_{2}}$ زمانی با یکدیگر یکسان است که:

$r=\sqrt{{{R}_{1}}{{R}_{2}}}\xrightarrow[{{R}_{1}}=4\Omega ]{r=2\Omega }2=\sqrt{4{{R}_{2}}}\Rightarrow {{R}_{2}}=1\Omega $