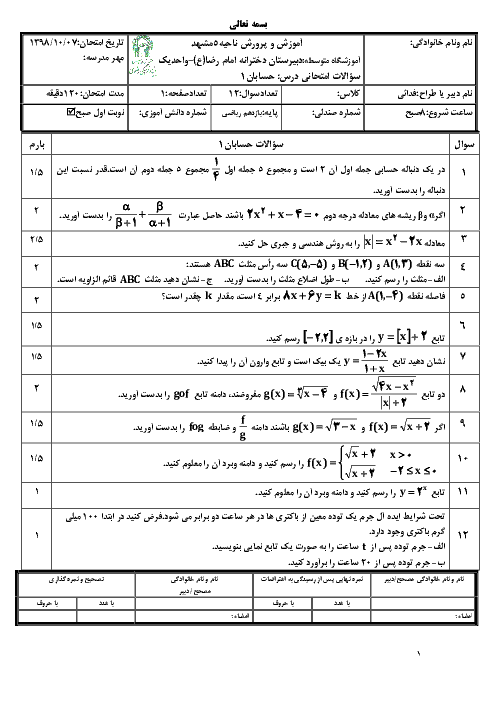
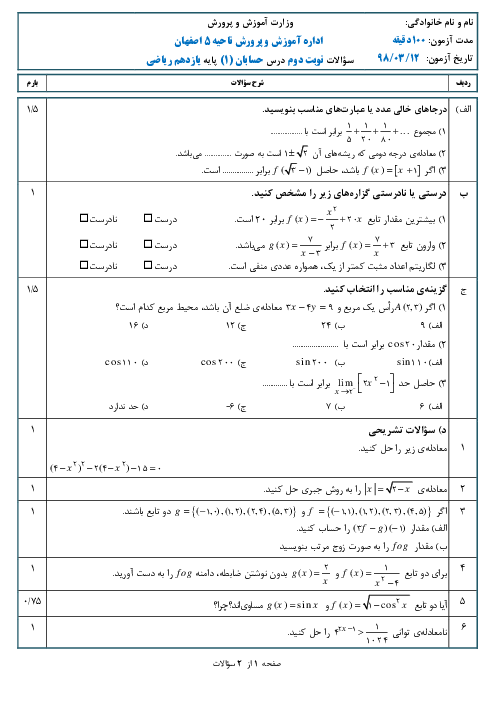
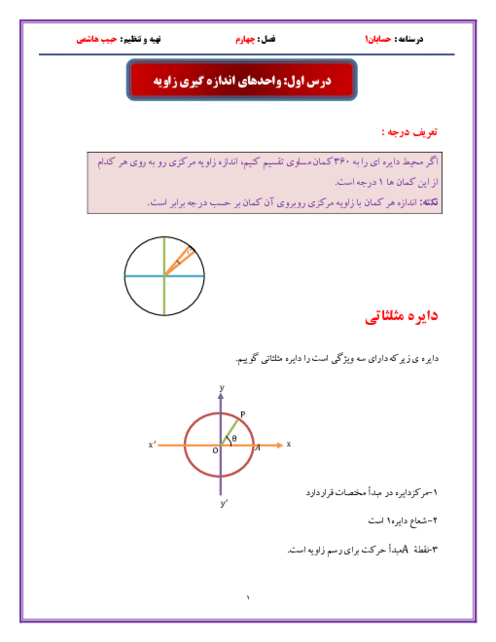
هرگاه $Cotg{15^ \circ } = 2 + \sqrt 3 $ حاصل کسر $\frac{{3\operatorname{Sin} {{75}^ \circ } + 2\operatorname{Sin} {{105}^ \circ }}}{{\operatorname{Cos} {{165}^ \circ } - \operatorname{Cos} {{255}^ \circ }}}$ را حساب کنید.
پاسخ تشریحی :
$\eqalign{
& p = \frac{{3\operatorname{Sin} (90 - {{15}^ \circ }) + 2\operatorname{Sin} (90 + {{15}^ \circ })}}{{\operatorname{Cos} (180 - {{15}^ \circ }) - \operatorname{Cos} (270 - {{15}^ \circ })}} = \frac{{3\operatorname{Cos} {{15}^ \circ } + 2\operatorname{Cos} {{15}^ \circ }}}{{ - \operatorname{Cos} {{15}^ \circ } + \operatorname{Sin} {{15}^ \circ }}} = \frac{{5\operatorname{Cos} {{15}^ \circ }}}{{ - \operatorname{Cos} {{15}^ \circ } + \operatorname{Sin} {{15}^ \circ }}} \cr
& = \frac{{5Cotg15}}{{ - Cotg15 + 1}} = \frac{{5(2 + \sqrt 3 )}}{{ - (2 + \sqrt 3 ) + 1}} = \frac{{5(2 + \sqrt 3 )}}{{ - 1 - \sqrt 3 }} \cr
& = \frac{{5(2 + \sqrt 3 )( - 1 + \sqrt 3 )}}{{( - 1 - \sqrt 3 )( - 1 + \sqrt 3 )}} = \frac{{5(\sqrt 3 + 1)}}{{1 - 3}} = \frac{{ - 5}}{2}(\sqrt 3 + 1) \cr} $
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!