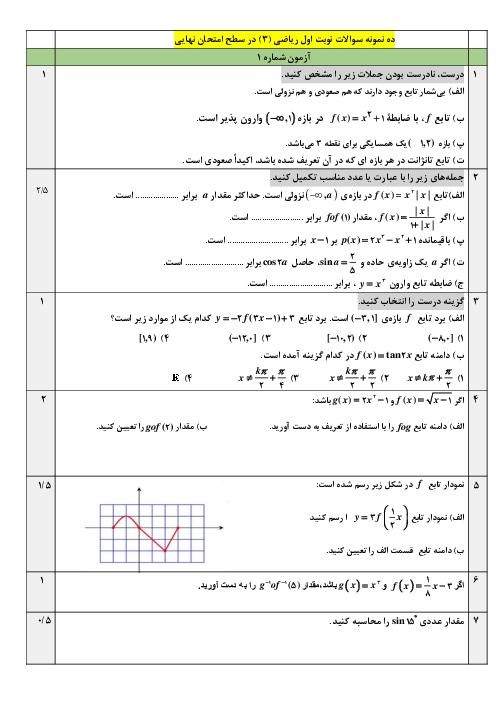
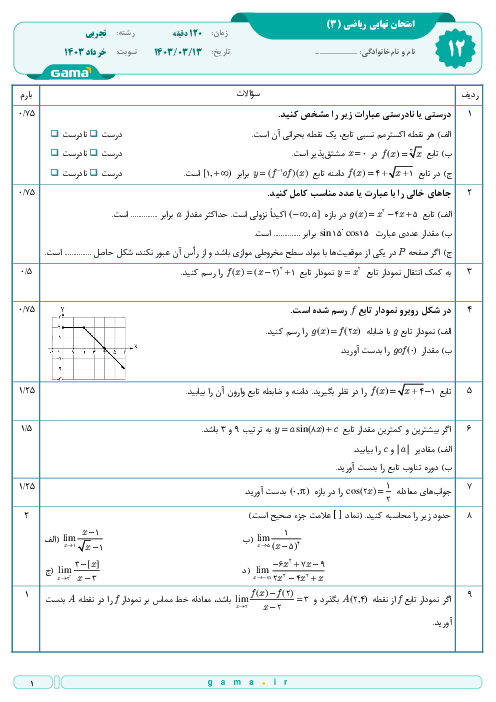
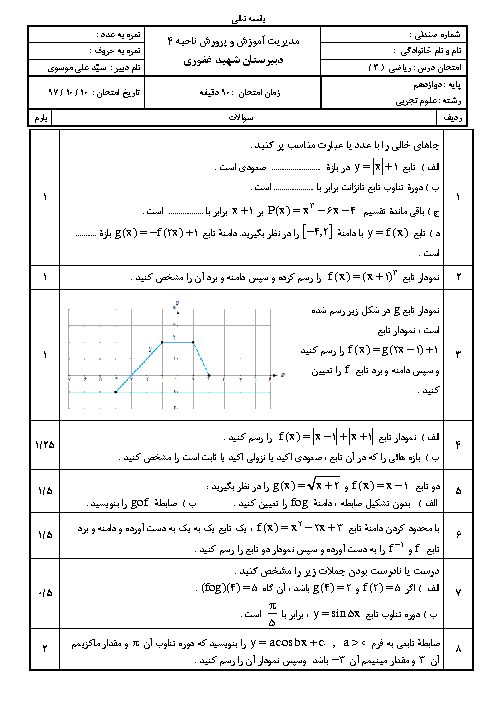
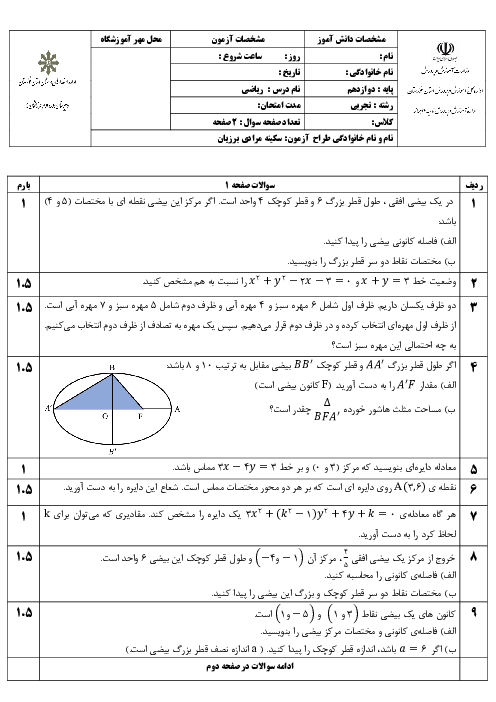
درس 1: تفکر تجسمی و آشنایی با مقاطع مخروطی
ریاضی (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم تجربی
درسنامه آموزشی این مبحث
از داخل یک استوانهٔ قائم توپر، به شعاع قاعدهٔ $4$ و ارتفاع $5$ واحد، بزرگ‌ترین مخروط قائم ممکن را حذف می‌کنیم. جسم حاصل را با صفحه‌ای موازی قاعدهٔ مخروط به فاصلهٔ $3$ واحد از آن قطع می‌دهیم. مساحت مقطع حاصل، کدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...