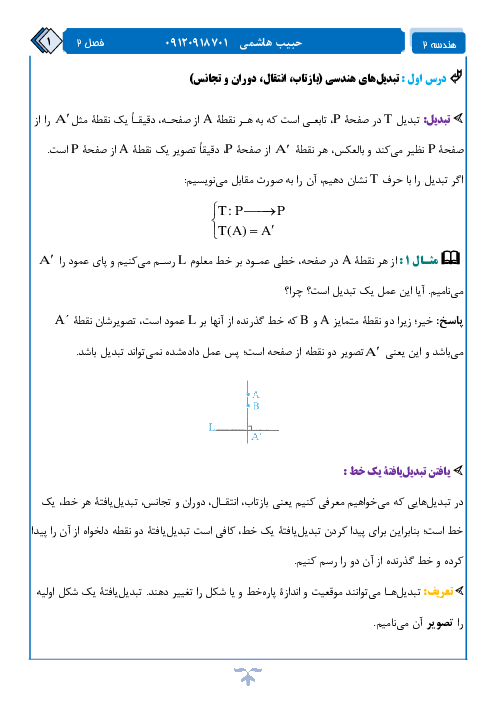
فصل 2: تبدیلهای هندسی و کاربردها
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
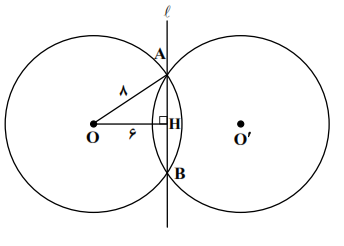
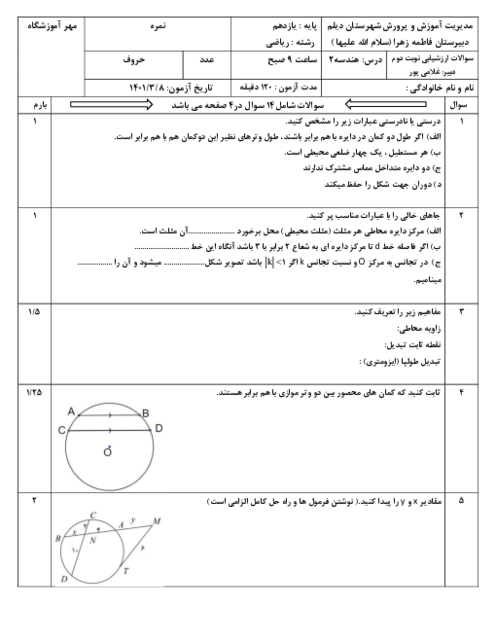
دو دایره به شعاع 8 بازتاب یکدیگرند. اگر فاصلهی مرکز هر دایره تا محور بازتاب 6 واحد باشد، طول وتر مشترک این دو دایره کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!