نكته: فرض كنيم تابع $f$ بر بازه‌ای مانند $(I\in {{D}_{f}})I$ پیوسته باشد و $c\in I$ یک نقطهٔ بحرانی تابع $f$ باشد. هر گاه $f$ بر این بازه به‌جز احتمالاً در نقطهٔ $c$، مشتق‌پذیر باشد، در این صورت:

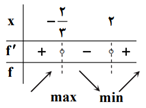
الف) اگر به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(a,c)$، ${f}'(x)\gt 0$ و به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(c,b)$، ${f}'(x)\lt 0$، در اين صورت $f(c)$ يک مقدار ماكزيمم نسبی $f$ است.

ب) اگر به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(a,c)$، ${f}'(x)\lt 0$ و به‌ازای تمام مقادير $x$ در بازه‌ای مانند $(c,b)$، ${f}'(x)\gt 0$، در اين صورت $f(c)$ يک مقدار مينيمم نسبی $f$ است.

پ) اگر ${f}'$ در نقطۀ $c$ تغيير علامت ندهد، به‌طوری كه ${f}'$ در هر دو طرف $c$ مثبت يا هر دو طرف آن منفی باشد، آنگاه $f(c)$ نه مينيمم نسبی و نه ماكزيمم نسبی است.

ابتدا ریشه‌های تابع ${f}'$ را محاسبه می‌کنیم:

${f}'(x)=3{{x}^{2}}-4x-4=(x-2)(3x+2)$

${f}'(x)=0\Rightarrow x=2,x=-\frac{2}{3}$

به‌كمک آزمون مشتق اول داريم:

طول نقطۀ مينيمم برابر ۲ است. پس اگر $f$ را ۲ واحد به چپ منتقل كنيم، نقطۀ مينيمم روی محور $y$ قرار می‌گیرد بنابراین: $a=2$