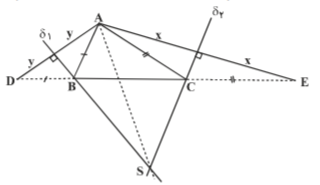
مرکز دایرهٔ محیطی مثلث $ADE$‌ نقطهٔ همرسی عمود منصف‌های اضلاع آن است. مطابق شکل، عمود منصف‌های $AD$ و $AE$ را رسم كرده‌ايم تا يک ديگر را در $S$ قطع کنند، $S$ مرکز دایرهٔ محیطی مثلث $ADE$‌ است. از طرفی، در دو مثلث متساوی‌الساقین $BAD$ و $CAE$، عمودمنصف‌های قاعده‌های $AD$ و $AE$، همان نیمسازهای زاویه‌های روبه‌روی قاعده، یعنی $A\hat{B}D$ و $A\hat{C}E$ هستند، به عبارت دیگر می‌توان گفت كه نيمسازهای زاويه‌های خارجی $B$ و $C$ بر ${{\partial }_{1}}$ بر ${{\partial }_{2}}$ واقع هستند و می‌دانيم كه در هر مثلث، هر دو نيمساز خارجی و نيمساز داخلی زاويهٔ سوم همرسند، يعنی $S$ روی امتداد نيمساز داخلی زاويهٔ $A$ واقع است.